题目内容

10．若命题p：0是偶数，命题q：2是3的约数，则下列命题中为真的是（　　）
A．p且qB．p或qC．非pD．以上都不对

分析 先判断出命题p与q的真假，再利用复合命题真假的判定方法即可得出．

解答 解：命题p：0是偶数，是真命题；
命题q：2是3的约数，是假命题．
则下列命题中为真的是p或q，
故选：B．

点评 本题考查了复合命题真假的判定方法、实数的性质，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
15．已知不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{x-4y+1≤0}\end{array}\right.$所表示的平面区域为M，不等式组$\left\{\begin{array}{l}{2x-3y-3≥0}\\{2x+2y-3≤0}\end{array}\right.$所表示的平面区域为N，若M中存在点在圆C：（x-3）2+（y-1）2=r2（r＞0）内，但N中不存在点在圆C内．则r的取值范围是（　　）
A．（0，$\frac{\sqrt{13}}{2}$]B．（$\frac{\sqrt{13}}{2}$，$\sqrt{17}$）C．（0，$\sqrt{17}$）D．（0，$\frac{5\sqrt{2}}{4}$）
16．$\sqrt{2-2cos8}$+2$\sqrt{1-sin8}$的化简结果是2cos4-4sin4．
13．首项为-12的等差数列从第20项起开始为正数，则公差d满足（　　）
A．d＞$\frac{12}{19}$B．d＜$\frac{2}{3}$C．$\frac{12}{19}$≤d＜$\frac{2}{3}$D．$\frac{12}{19}$＜d≤$\frac{2}{3}$
5．设a是函数$f（x）={2^x}-{log_{\frac{1}{2}}}$x的零点，若x0＞a，则f（x0）的值满足（　　）
A．f（x0）=0B．f（x0）＜0C．f（x0）＞0D．f（x0）的符号不确定
15．经过圆x2+y2+2y=0的圆心且与直线x+2y-2=0平行的直线方程是（　　）
A．x+2y-1=0B．x+2y+2=0C．x+2y+1=0D．x+2y+3=0
2．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个焦点为F（3，0），且双曲线的渐进线与圆（x-3）2+y2=1相切，则该双曲线的标准方程为$\frac{{x}^{2}}{8}$-y2=1..
19．从符号∈、∉、=、⊆、?≠中选出适当的一个填空
①a∈{a}；
②{1，2}={2，1}；
③a∉{（a，b）}；
④∅?{a}；
⑤{1，2}⊆{1，2，3}．
20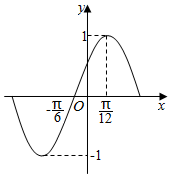．如图是某函数图象的一部分，则该函数表达式是（　　）
A．$y=cos（\frac{π}{6}-2x）$B．$y=cos（2x-\frac{π}{3}）$C．$y=sin（x+\frac{π}{6}）$D．$y=sin（2x-\frac{π}{6}）$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网