题目内容
 在长方体ABCD-A1B1C1D1中,AB=AD=3,AA1=4,E为AA1的中点.
在长方体ABCD-A1B1C1D1中,AB=AD=3,AA1=4,E为AA1的中点.(Ⅰ)证明:A1C∥平面BDE;
(Ⅱ)求三棱锥D1-BDE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)连结AC,BD,交于点O,连结EO,由已知条件得A1C∥OE,由此能证明A1C∥平面BDE.
(Ⅱ)由VD1-BDE=VB-DED1,利用等积法能求出三棱锥D1-BDE的体积.
(Ⅱ)由VD1-BDE=VB-DED1,利用等积法能求出三棱锥D1-BDE的体积.
解答:
(Ⅰ)证明:连结AC,BD,交于点O,连结EO,
∵长方体ABCD-A1B1C1D1中,ABCD是长方形,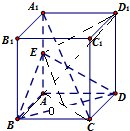
∴O是AC中点,又E是AA1的中点,
∴A1C∥OE,
∵OE?平面BDE,A1C不包含于平面BDE,
∴A1C∥平面BDE.
(Ⅱ)解:∵在长方体ABCD-A1B1C1D1中,
AB=AD=3,AA1=4,E为AA1的中点,
B到平面DED1的距离h=AB=3,
S△DED1=
×3×4=6,
∴VD1-BDE=VB-DED1=
×h×S△DED1
=
×3×6=6.
∵长方体ABCD-A1B1C1D1中,ABCD是长方形,

∴O是AC中点,又E是AA1的中点,
∴A1C∥OE,
∵OE?平面BDE,A1C不包含于平面BDE,
∴A1C∥平面BDE.
(Ⅱ)解:∵在长方体ABCD-A1B1C1D1中,
AB=AD=3,AA1=4,E为AA1的中点,
B到平面DED1的距离h=AB=3,
S△DED1=
| 1 |
| 2 |
∴VD1-BDE=VB-DED1=
| 1 |
| 3 |
=
| 1 |
| 3 |
点评:本题考查直线与平面平行的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若向量
,
为两个非零向量,且|
|=|
|=|
+
|,则向量
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
 某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线l相切于点M.A为上半圆弧上一点,过点A作l的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:m2),∠AON=θ(单位:弧度).
某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线l相切于点M.A为上半圆弧上一点,过点A作l的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:m2),∠AON=θ(单位:弧度).