题目内容
设p:实数x满足x2-4ax+3a2<0(其中a≠0),q:实数x满足
<0.
(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若p是q的必要不充分条件,求实数a的取值范围.
| x-3 |
| x-2 |
(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若p是q的必要不充分条件,求实数a的取值范围.
考点:复合命题的真假
专题:计算题,简易逻辑
分析:(Ⅰ)若a=1,由题意知,p、q为真,从而求p、q都为真时x的范围;
(Ⅱ)由p是q的必要不充分条件可知B?A,讨论a的正负以确定集合A,从而求实数a的取值范围.
(Ⅱ)由p是q的必要不充分条件可知B?A,讨论a的正负以确定集合A,从而求实数a的取值范围.
解答:
解:(I)当a=1时,p为真时实数x的取值范围是1<x<3,
q为真时实数x的取值范围是2<x<3.
若p∧q为真,则p真且q真,
∴实数x的取值范围是(2,3).
(II)设A={x|p(x)},B={x|q(x)}=(2,3),
∵p是q的必要不充分条件,
∴B?A,
由x2-4ax+3a2<0得(x-3a)(x-a)<0
当a>0时,A=(a,3a),有
,解得1≤a≤2;
当a<0时,A=(3a,a),显然A∩B=∅,不合题意.
∴实数a的取值范围是1≤a≤2.
q为真时实数x的取值范围是2<x<3.
若p∧q为真,则p真且q真,
∴实数x的取值范围是(2,3).
(II)设A={x|p(x)},B={x|q(x)}=(2,3),
∵p是q的必要不充分条件,
∴B?A,
由x2-4ax+3a2<0得(x-3a)(x-a)<0
当a>0时,A=(a,3a),有
|
当a<0时,A=(3a,a),显然A∩B=∅,不合题意.
∴实数a的取值范围是1≤a≤2.
点评:本题考查了复合命题真假性的应用及集合的包含关系的应用,属于基础题.

练习册系列答案
相关题目
函数y=
(0<φ<
)的图象如图,则( )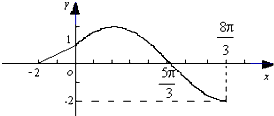
|
| π |
| 2 |

A、k=
| ||||||
B、k=
| ||||||
C、k=-
| ||||||
D、k=-2,ω=2,φ=
|
 已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.函数f(x)在y轴左侧的图象如图所示.
已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.函数f(x)在y轴左侧的图象如图所示.