题目内容
小乐星期六下午从文具超市买了一套立体几何学具,他发现学具袋里有三组长度相等的塑料棒,长度分别为1,
,2,而且每组恰有三根,于是想利用它们拼出正三棱锥.设拼出的正三棱锥的侧棱长为l,底面正三角形的边长为s.
(1)若小乐选取l=1,s=
,现从该正三棱锥的六条棱中随机选取两条,求这两条棱互相垂直的概率;
(2)若小乐随机地选取l,s,可以拼出m个不同的正三棱锥.设从每个正三棱锥的六条棱中随机选取两条,这两条棱互相垂直的概率为X,请分别写出其相应的X的值(不用写出求解X的计算过程).小乐再从拼出的m个正三棱锥中任选两个,求他所选的两个正三棱锥的X值相同的概率.
| 2 |
(1)若小乐选取l=1,s=
| 2 |
(2)若小乐随机地选取l,s,可以拼出m个不同的正三棱锥.设从每个正三棱锥的六条棱中随机选取两条,这两条棱互相垂直的概率为X,请分别写出其相应的X的值(不用写出求解X的计算过程).小乐再从拼出的m个正三棱锥中任选两个,求他所选的两个正三棱锥的X值相同的概率.
考点:离散型随机变量的期望与方差,棱锥的结构特征
专题:应用题,概率与统计
分析:(1)利用列举法确定从该正三棱锥的六条棱中随机选取两条的选法,两条棱互相垂直的选法,利用古典概型的概率公式,可得结论;
(2)确定可以拼出5个正三棱锥,可得从中任选两个,共有10种选法,所选的两个正三棱锥的X值相同共有4种选法,即可求出他所选的两个正三棱锥的X值相同的概率.
(2)确定可以拼出5个正三棱锥,可得从中任选两个,共有10种选法,所选的两个正三棱锥的X值相同共有4种选法,即可求出他所选的两个正三棱锥的X值相同的概率.
解答:
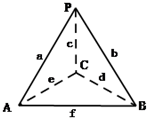 解:(1)如图,设小乐所拼的正三棱锥P-ABC的三条侧棱分别记为a,b,c,底面正三角形ABC的三边分别记为d,e,f,
解:(1)如图,设小乐所拼的正三棱锥P-ABC的三条侧棱分别记为a,b,c,底面正三角形ABC的三边分别记为d,e,f,
从该正三棱锥的六条棱中随机选取两条,共有15种选法,分别为:(a,b),(a,c),(a,d),(a,e),(a,f)(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)…(3分)
因为l=1,s=
,由勾股定理可知∠APB=∠APC=∠BPC=90°,
又正三棱锥的对棱互相垂直,所以其中两条棱互相垂直的选法共有6种,分别为:(a,b),(b,c),(a,c),(a,d),(b,e),(c,f),
记事件“两条棱互相垂直”为A,所以所求概率为P(A)=
=
.…(6分)
(2)由题意,l=1,s=2时不能拼成正三棱锥,所以可以拼出5个正三棱锥,依次为
①l=1,s=
,X=
;②l=
,s=1,X=
;③l=
,s=2,X=
;
④l=2,s=1,X=
;⑤l=2,s=
,X=
;
从中任选两个,共有10种选法,所选的两个正三棱锥的X值相同共有4种选法,
所以他所选的两个正三棱锥的X值相同的概率为
=
.
 解:(1)如图,设小乐所拼的正三棱锥P-ABC的三条侧棱分别记为a,b,c,底面正三角形ABC的三边分别记为d,e,f,
解:(1)如图,设小乐所拼的正三棱锥P-ABC的三条侧棱分别记为a,b,c,底面正三角形ABC的三边分别记为d,e,f,从该正三棱锥的六条棱中随机选取两条,共有15种选法,分别为:(a,b),(a,c),(a,d),(a,e),(a,f)(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)…(3分)
因为l=1,s=
| 2 |
又正三棱锥的对棱互相垂直,所以其中两条棱互相垂直的选法共有6种,分别为:(a,b),(b,c),(a,c),(a,d),(b,e),(c,f),
记事件“两条棱互相垂直”为A,所以所求概率为P(A)=
| 6 |
| 15 |
| 2 |
| 5 |
(2)由题意,l=1,s=2时不能拼成正三棱锥,所以可以拼出5个正三棱锥,依次为
①l=1,s=
| 2 |
| 2 |
| 5 |
| 2 |
| 1 |
| 5 |
| 2 |
| 2 |
| 5 |
④l=2,s=1,X=
| 1 |
| 5 |
| 2 |
| 1 |
| 5 |
从中任选两个,共有10种选法,所选的两个正三棱锥的X值相同共有4种选法,
所以他所选的两个正三棱锥的X值相同的概率为
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查概率的计算,考查列举法确定基本事件,正确确定基本事件的个数是关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知圆C:(x-l)2+y2=l与直线l:x-2y+1=0相交于A、B两点,则|AB|=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
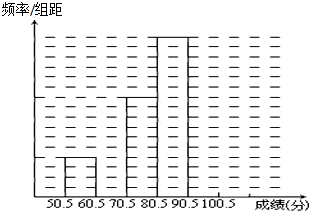 某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题: 如图是计算1+2+
如图是计算1+2+