题目内容
17.已知点M(4,0),点P在曲线y2=8x上运动,点Q在曲线(x-2)2+y2=1上运动,则$\frac{|PM{|}^{2}}{|PQ|}$取到最小值时P的横坐标为2.分析 设圆心为F,则容易知道F为抛物线y2=8x的焦点,并且$\frac{|PM{|}^{2}}{|PQ|}$最小时,PM经过圆心F,设P(x,y),则:
|PM|2=(x-4)2+y2=(x-4)2+8x=x2+16,|PQ|=x+2+1=x+3,所以$\frac{|PM{|}^{2}}{|PQ|}$=$\frac{{x}^{2}+16}{x+3}$,求$\frac{{x}^{2}+16}{x+3}$的最小值即可.
解答 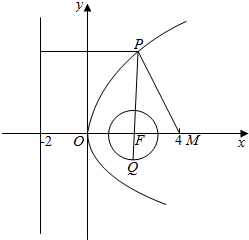 解:如图,设圆心为F,则F为抛物线y2=8x的焦点,该抛物线的准线方程为x=-2,设P(x,y),
解:如图,设圆心为F,则F为抛物线y2=8x的焦点,该抛物线的准线方程为x=-2,设P(x,y),
由抛物线的定义:|PF|=x+2,要使$\frac{|PM{|}^{2}}{|PQ|}$最小,则|PQ|需最大,如图,|PQ|最大时,经过圆心F,且圆F的半径为1,∴|PQ|=|PF|+1=x+3,且|PM|=$\sqrt{(x-4)^{2}+{y}^{2}}$=$\sqrt{{x}^{2}+16}$
∴$\frac{|PM{|}^{2}}{|PQ|}$=$\frac{{x}^{2}+16}{x+3}$,
令x+3=t(t≥3),则x=t-3,
∴$\frac{|PM{|}^{2}}{|PQ|}$=t+$\frac{25}{t}$-6≥4,当t=5时取“=“;
此时x=2.
故答案为:2.
点评 考查抛物线的标准方程,焦点坐标公式,准线方程,及抛物线的定义,圆的标准方程,利用基本不等式求函数的最值.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
8.在数列{an}中,已知a1=3,当n≥2时,$\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}}=\frac{1}{5},{a_{16}}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
 中, 斜率为
中, 斜率为 的直线交椭圆于左顶点
的直线交椭圆于左顶点 和另一点
和另一点 ,点
,点 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点 ,若椭圆离心率
,若椭圆离心率 ,则
,则 的值为_ .
的值为_ .