题目内容
12.设偶函数f(x)(x∈R)满足f(x)=f(2-x),且当x∈[0,1]时,f(x)=x2.又函数g(x)=|cos(πx)|,则函数h(x)=g(x)-f(x)在区间$[{-\frac{1}{2},\frac{3}{2}}]$上的零点个数为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 根据条件可得f(x)是周期函数,T=2,且是偶函数,令h(x)=0,则f(x)=g(x),在同一坐标系中作y=f(x)和y=g(x)在区间$[{-\frac{1}{2},\frac{3}{2}}]$上的图象,由图象可得结论.
解答 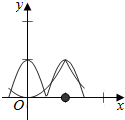 解:∵f(x)=f(2-x),故f(x)的图象关于x=1对称,
解:∵f(x)=f(2-x),故f(x)的图象关于x=1对称,
又函数f(x)是R上的偶函数,∴f(x+2)=f(-x)=f(x),
∴f(x)是周期函数,T=2,
当x∈[-1,0]时,f(x)=f(-x)=x2.
令h(x)=0,则f(x)=g(x),
在同一坐标系中作y=f(x)和y=g(x)在区间$[{-\frac{1}{2},\frac{3}{2}}]$上的图象,
由图象可得y=f(x)和y=g(x)有5个交点,
故函数h(x)=f(x)-g(x)的零点个数为5.
故选:A.
点评 本题考查函数零点的定义,体现了数形结合的数学思想,在同一坐标系中作y=f(x)和y=g(x)的图象,是解题的关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.全集U={x∈Z|0<x≤8},M={1,3,5,7},N={5,6,7},则∁U(M∪N)=( )
| A. | {5,7} | B. | {2,4} | C. | {2,4,8} | D. | {1,3,5,6,7} |
7.已知命题p:“?x∈[0,1],a≥ex”;命题q:“?x0∈R,x${\;}_{0}^{2}$+4x0+a=0”.若命题“p∧q”是假命题,则实数a的取值范围是( )
| A. | (-∞,4] | B. | (-∞,1)∪(4,+∞) | C. | (-∞,e)∪(4,+∞) | D. | (1,+∞) |
 中,
中, ,
, 为
为 中点, 点
中点, 点 分别为
分别为 的中点, 将
的中点, 将 沿
沿 折起到
折起到  的位置,使得平面
的位置,使得平面 平面
平面 (如图
(如图  ).
).

 ;
; 与平面
与平面 所成角的正弦值;
所成角的正弦值; 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.