题目内容
已知P′为直线x+y-1=0上任意一点，连接P′O并延长至P，使|P′O|•|OP|=4，求P点的轨迹方程．
考点：轨迹方程
专题：计算题,直线与圆
分析：以原点O为极点，Ox为极轴，建立极坐标系，可得直线方程的极坐标方程，由已知ρ′•ρ=4，即ρ′=
，即可求P点的轨迹方程．
| 4 |
| ρ |
解答：
解：以原点O为极点，Ox为极轴，建立极坐标系
则直线方程化为极坐标方程为：ρcosθ+ρsinθ-1=0．
设P′（ρ′，θ）、P（ρ，θ），
由已知ρ′•ρ=4，即ρ′=
．
代入直线的极坐标方程得：
cosθ+
sinθ-1=0．
即ρ=4cosθ+4sinθ，
化为直角坐标方程：（x-2）2+（y-2）2=8（除去原点）．
则直线方程化为极坐标方程为：ρcosθ+ρsinθ-1=0．
设P′（ρ′，θ）、P（ρ，θ），
由已知ρ′•ρ=4，即ρ′=
| 4 |
| ρ |
代入直线的极坐标方程得：
| 4 |
| ρ |
| 4 |
| ρ |
即ρ=4cosθ+4sinθ，
化为直角坐标方程：（x-2）2+（y-2）2=8（除去原点）．
点评：本题考查轨迹方程，考查极坐标方程，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=
•
的定义域是（ ）
| 4-x |
| x+1 |
| A、[-1，+∞） |
| B、（-∞，-1] |
| C、[-1，4] |
| D、（-1，4） |
设底面为等边三角形的直棱柱的体积为V，则其表面积最小时，底面边长为（ ）
A、
| |||
B、
| |||
C、
| |||
D、
|
棱长为a的正方体内切一球，该球的表面积为（ ）
| A、πa2 |
| B、2πa2 |
| C、3πa2 |
| D、4πa2 |
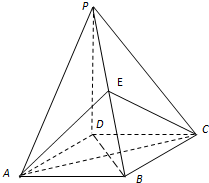如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上．