Question

在△ABC中，BC=

2

，AC=1，以AB为边作等腰直角三角形ABD（B为直角顶点，C、D两点在直线AB的两侧）．当∠C变化时，线段CD长的最大值为（　　）

• A、1
• B、2
• C、3
• D、4

Answer 1

考点：余弦定理

专题：解三角形

分析：在△ABC中，由正弦定理得BDsin∠ABC=sin∠ACB，在△BCD，△ABC中由余弦定理可得CD²=BD²+BC²-2BD•BCcos（90°+∠ABC）=AC²+BC²-2AC•BCcos∠ACB+2+2

2

sin∠ACB，可化为5+4sin（∠ACB-45°），由此可求答案．

解答： 解：如右图：△ABC中，BC=

2

，AC=1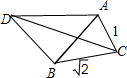，∵AB=BD，
∴在△ABC中，由正弦定理得

AC

sin∠ABC

=

AB

sin∠ACB

=

BD

sin∠ACB

，
∴BDsin∠ABC=sin∠ACB，
在△BCD中，CD²=BD²+BC²-2BD•BCcos（90°+∠ABC）
=AB²+2+2AB•

2

sin∠ABC
=（ AC²+BC²-2AC•BC•cos∠ACB）+2+2

2

•ABsin∠ABC
=（1+2-2

2

cos∠ACB）+2+2

2

•BDsin∠ABC
=（1+2-2

2

cos∠ACB）+2+2

2

•sin∠ACB
=5+2

2

•sin∠ACB-2

2

cos∠ACB
=5+4sin（∠ACB-45°），
∴当∠ACB=135°时CD²最大为9，故CD最大值为3，
故选：C．

点评：该题主要考查正弦定理、余弦定理及其应用，考查三角函数的恒等变换，属中档题．