题目内容
已知直线l：y=x-1和圆C：x2+y2-6x+4y+4=0交于M，N两点．
（Ⅰ）求|MN|；
（Ⅱ）求以线段MN为直径的圆P的方程．
（Ⅰ）求|MN|；
（Ⅱ）求以线段MN为直径的圆P的方程．
考点：直线和圆的方程的应用
专题：计算题,直线与圆
分析：（Ⅰ）求出圆心C的坐标，C到直线y=x-1的距离，即可求|MN|；
（Ⅱ）求出以线段MN为直径的圆P的圆心坐标，即可求出以线段MN为直径的圆P的方程．
（Ⅱ）求出以线段MN为直径的圆P的圆心坐标，即可求出以线段MN为直径的圆P的方程．
解答：
解：（Ⅰ）圆C：x2+y2-6x+4y+4=0的方程变为：（x-3）2+（y+2）2=9，
∴C到直线y=x-1的距离d=2
，
∴|MN|=2
=2；
（Ⅱ）与直线y=x-1垂直的直径所在直线方程是x+y-1=0，联立方程，可得交点P（1，0），
∵|MN|=2，
∴以线段MN为直径的圆P的方程为（x-1）2+y2=1．
∴C到直线y=x-1的距离d=2
| 2 |
∴|MN|=2
| 9-8 |
（Ⅱ）与直线y=x-1垂直的直径所在直线方程是x+y-1=0，联立方程，可得交点P（1，0），
∵|MN|=2，
∴以线段MN为直径的圆P的方程为（x-1）2+y2=1．
点评：考查学生综合运用直线与圆方程的能力，考查学生分析解决问题的能力，难度中等．
练习册系列答案
相关题目
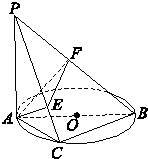如图所示，已知PA⊥⊙O所在平面，AB是⊙O的直径，点C是⊙O上任意一点，过A作AE⊥PC于点E，AF⊥PB于点F，求证：
已知一几何体的三视图如图所示，点F，G分别为AC，DE的中点．