题目内容
若曲线C1:x2+y2-2x=0与曲线C2:y(y-mx-m)=0有三个不同的交点,则实数m的值为 .
考点:曲线与方程,圆的一般方程
专题:直线与圆
分析:把圆的方程化为标准方程,求出圆心和半径,直线过定点(-1,0),当直线y-mx-m=0与圆相切时,根据圆心到直线的距离d=
=r=1,求出m的值,数形结合求出实数m的取值范围.
| |-m| | ||
|
解答:
解:由题意可知曲线C1:x2+y2-2x=0表示一个圆,化为标准方程得: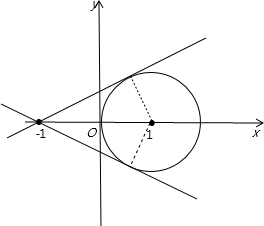
(x-1)2+y2=1,所以圆心坐标为(1,0),半径r=1;
C2:y(y-mx-m)=0表示两条直线y=0和y-mx-m=0,直线y=0与曲线C1:x2+y2-2x=0有两个交点
由直线y-mx-m=0可知:此直线过定点(-1,0),
在平面直角坐标系中画出图象如图所示:
当直线y-mx-m=0与圆相切时,圆心到直线的距离d=
=r=1,
化简得:m2=
,m=±
.直线与圆相切是,两曲线有3分交点,直线y-mx-m=0经过原点是只有2个交点,
曲线C1:x2+y2-2x=0与曲线C2:y(y-mx-m)=0有三个不同的交点,m=±
.
故答案为:±
.

(x-1)2+y2=1,所以圆心坐标为(1,0),半径r=1;
C2:y(y-mx-m)=0表示两条直线y=0和y-mx-m=0,直线y=0与曲线C1:x2+y2-2x=0有两个交点
由直线y-mx-m=0可知:此直线过定点(-1,0),
在平面直角坐标系中画出图象如图所示:
当直线y-mx-m=0与圆相切时,圆心到直线的距离d=
| |-m| | ||
|
化简得:m2=
| 1 |
| 3 |
| ||
| 3 |
曲线C1:x2+y2-2x=0与曲线C2:y(y-mx-m)=0有三个不同的交点,m=±
| ||
| 3 |
故答案为:±
| ||
| 3 |
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若双曲线x2-
=1的一个焦点与抛物线y2=8x的焦点重合,则此双曲线的渐近线方程为( )
| y2 |
| m |
| A、x±y=0 | ||
B、
| ||
C、
| ||
D、
|