题目内容
已知焦点在x轴上的双曲线的渐近线为y=±2x,则此双曲线的离心率为 .
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出双曲线的方程,求出渐近线方程,得到b=2a,再由a,b,c的关系,结合离心率公式,即可得到.
解答:
解:设双曲线的方程为
-
=1,(a,b>0),
则渐近线方程为y=±
x,
即有2=
,则b=2a,
c=
=
a,
则e=
=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
则渐近线方程为y=±
| b |
| a |
即有2=
| b |
| a |
c=
| a2+b2 |
| 5 |
则e=
| c |
| a |
| 5 |
故答案为:
| 5 |
点评:本题考查双曲线的方程和性质,主要是渐近线和离心率的求法,考查运算能力,属于基础题.

练习册系列答案
相关题目
利用计算机产生0~1之间的均匀随机数a,则事件“4a-1<0”发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知P(-2,0)、Q(2,0)若点M是抛物线y2=4x上的动点,则
的最大值为( )
| |MP| |
| |MQ| |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
xOy平面内点的坐标的特点是( )
| A、z坐标是0 |
| B、x坐标和y坐标都是0 |
| C、x坐标是0 |
| D、x坐标,y坐标和z坐标不可能都是0 |
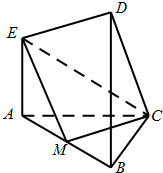 如图,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点
如图,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点