题目内容
已知函数f(x)=x+
,x∈[1,3].
(1)试判断f(x)在[1,2]和[2,3]上的单调性;
(2)根据f(x)的单调性写出f(x)的最值.
| 4 |
| x |
(1)试判断f(x)在[1,2]和[2,3]上的单调性;
(2)根据f(x)的单调性写出f(x)的最值.
考点:函数的最值及其几何意义,函数单调性的判断与证明
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求导f′(x)=1-
=
,由导数的正负确定函数的单调性;
(2)由单调性求端点函数值及极值,从而求最值.
| 4 |
| x2 |
| (x+2)(x-2) |
| x2 |
(2)由单调性求端点函数值及极值,从而求最值.
解答:
解:(1)f′(x)=1-
=
;
故当x∈[1,2]时,f′(x)≤0,当x∈[2,3]时,f′(x)≥0;
故f(x)在[1,2]上是减函数,在[2,3]上是增函数;
(2)由单调性知,
f(1)=1+4=5,f(3)=3+
=
,f(2)=2+2=4;
故f(x)的最大值为5,最小值为4.
| 4 |
| x2 |
| (x+2)(x-2) |
| x2 |
故当x∈[1,2]时,f′(x)≤0,当x∈[2,3]时,f′(x)≥0;
故f(x)在[1,2]上是减函数,在[2,3]上是增函数;
(2)由单调性知,
f(1)=1+4=5,f(3)=3+
| 4 |
| 3 |
| 13 |
| 3 |
故f(x)的最大值为5,最小值为4.
点评:本题考查了导数的综合应用,属于基础题.

练习册系列答案
相关题目
设P是双曲线
-
=1(a>0)右支上一点,其一条渐近线方程是3x-2y=0,F1、F2分别是双曲线的左、右焦点,若|PF1|=8,则|PF2|等于( )
| x2 |
| a2 |
| y2 |
| 9 |
| A、4 | B、12 |
| C、4或12 | D、2或14 |
执行如图所示的程序框图,输出的S是( )


| A、10 | B、15 | C、20 | D、35 |
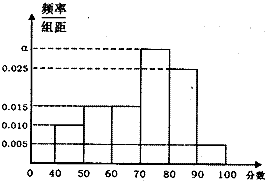 某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.
某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.