题目内容
（1）已知tan α=
，求
的值；
（2）化简：
．
| 1 |
| 3 |
| 1 |
| 2sinαcosα+cos2α |
（2）化简：
tan(π-α)cos(2π-α)sin(-α+
| ||
| cos(-α-π)sin(-π-α) |
考点：三角函数的化简求值,运用诱导公式化简求值
专题：计算题,三角函数的求值
分析：（1）所求式子分子“1”，利用同角三角函数间的基本关系化简为sin2α+cos2α，分子分母除以cos2α化简，将tanα的值代入计算即可求出值．
（2）直接利用诱导公式化简表达式，通过同角三角函数的基本关系式化简即可得到结果．
（2）直接利用诱导公式化简表达式，通过同角三角函数的基本关系式化简即可得到结果．
解答：
解：（1）∵tanα=
，
∴原式=
=
=
=
．
（2）
=
=
=-1．
| 1 |
| 3 |
∴原式=
| sin2α+cos2α |
| 2sinαcosα+cos2α-sin2α |
| tan2α+1 |
| 2tanα+1-tan2α |
| ||||
2×
|
| 5 |
| 7 |
（2）
tan(π-α)cos(2π-α)sin(-α+
| ||
| cos(-α-π)sin(-π-α) |
-tanαcos(-α)sin(α+
| ||
| -cosαsinα |
| ||
| -sinα |
点评：本题（1）考查了三角函数的化简求值，熟练掌握同角三角函数间的基本关系是解本题的关键，（2）考查诱导公式的应用，考查计算能力．
练习册系列答案
相关题目
已知几何体A-BCDE的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则该几何体的体积V的大小为已知函数f（x）的图象是连续不断的，有如下x，f（x）对应值表：
其中a＜c＜0＜b，则函数f（x）在区间[1，6]上零点至少有（ ）
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f（x） | 10 | 13 | c | 7 | a | b |
| A、2个 | B、3个 | C、4个 | D、5个 |
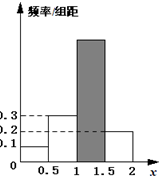如图所示的频率分布直方图，其中阴影部分的小长方形的高度是（ ）| A、0.4 | B、0.8 |
| C、1.4 | D、1.6 |
一个空间几何体的三视图及其相关数据如图所示，则这个空间几何体的表面积是（ ）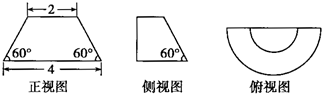
A、
| ||||
B、
| ||||
| C、11π | ||||
D、
|