题目内容
已知数列{an}中,a1=1,且当x=
时,函数f(x)=
an•x2+(2-n-an+1)•x取得极值.
(1)若bn=2n-1•an,求数列{bn}的通项公式;
(2)求数列{an}的前n项和Sn;
(3)试证明:n>3(n∈N*)时,Sn>
.
| 1 |
| 2 |
| 1 |
| 2 |
(1)若bn=2n-1•an,求数列{bn}的通项公式;
(2)求数列{an}的前n项和Sn;
(3)试证明:n>3(n∈N*)时,Sn>
| 4n |
| n+1 |
考点:数列与不等式的综合
专题:计算题,证明题,导数的综合应用,不等式的解法及应用
分析:(1)求出导数,由极值的定义,得f′(
)=0,得an+1=
an+2-n,由bn=2n-1•an,则bn+1-bn=1,由等差数列的通项公式即可得到;
(2)运用错位相减法求数列的和,注意解题步骤,运用等比数列求和公式即可得到;
(3)运用二项式定理,展开2n=(1+1)n,即可得证.
| 1 |
| 2 |
| 1 |
| 2 |
(2)运用错位相减法求数列的和,注意解题步骤,运用等比数列求和公式即可得到;
(3)运用二项式定理,展开2n=(1+1)n,即可得证.
解答:
(1)解:f′(x)=anx+2-n-an+1,
由题意得f′(
)=0,得an+1=
an+2-n,
由an+1=
an+2-n,得2nan+1-2n-1•an=1,
由bn=2n-1•an,则bn+1-bn=1,
则数列{bn}的通项公式bn=b1+(n-1)×1=1+n-1=n;
(2)解:由(1)得,an=n•21-n,
则Sn=1•21-1+2×21-2+3×21-3+…+(n-1)×21-(n-1)+n•21-n,
2Sn=1×2+2×21-1+3×21-2+…+n•22-n,
两式相减得,Sn=1×2+1×21-1+1×21-2+1×21-3+…+1×21-(n-1)-n•21-n
=
-n•21-n=4-
;
(3)证明:由Sn=4-
=4-
=4-
n>3时,Sn>4-
=4-
=4-
=
.
由题意得f′(
| 1 |
| 2 |
| 1 |
| 2 |
由an+1=
| 1 |
| 2 |
由bn=2n-1•an,则bn+1-bn=1,
则数列{bn}的通项公式bn=b1+(n-1)×1=1+n-1=n;
(2)解:由(1)得,an=n•21-n,
则Sn=1•21-1+2×21-2+3×21-3+…+(n-1)×21-(n-1)+n•21-n,
2Sn=1×2+2×21-1+3×21-2+…+n•22-n,
两式相减得,Sn=1×2+1×21-1+1×21-2+1×21-3+…+1×21-(n-1)-n•21-n
=
| 2(1-2-n) |
| 1-2-1 |
| 4+2n |
| 2n |
(3)证明:由Sn=4-
| 4+2n |
| 2n |
| 4+2n |
| (1+1)n |
| 4+2n | ||
1+n+
|
n>3时,Sn>4-
| 4+2n | ||
1+n+
|
| 4+2n | ||
|
| 4 |
| 1+n |
| 4n |
| n+1 |
点评:本题考查导数的运用:求极值,考查数列的通项公式的求法,注意构造数列,运用等差数列的通项公式和等比数列求和公式,考查错位相减求和,以及二项式定理用于证明不等式的方法,属于中档题和易错题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知等差数列{an}的前n项和为Sn,若S10<0,S11>0,则当Sn最小时n的值是( )
| A、7 | B、6 | C、5 | D、4 |
已知M,N为整合I的非空真子集,且M,N不相等,若N∩∁UM=φ,则M∪N是( )
| A、M | B、N | C、I | D、φ |
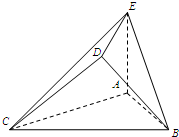 如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.