题目内容
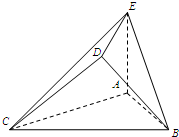 如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.(Ⅰ)求证:AE∥平面BCD;
(Ⅱ)求证:平面BDE⊥平面CDE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:根据面面垂直,线面垂直的判定定理从而进行证明.
解答:
证明:(Ⅰ)取BC的中点M,连接DM、AM,
因为BD=CD,且BD⊥CD,BC=2,
所以DM=1,DM⊥BC,AM⊥BC.
又因为平面BCD⊥平面ABC,
所以DM⊥平面ABC,
所以AE∥DM,
又因为AE?平面BCD,DM?平面BCD,
所以AE∥平面BCD.
(Ⅱ)由(Ⅰ)得:AE∥DM,又AE=1,DM=1,
∴四边形DMAE 是平行四边形,
∴DE∥AM,
由(Ⅰ)已证AM⊥BC,又∵平面BCD⊥平面ABC,
∴AM⊥平面BCD,
∴DE⊥平面BCD,
又CD?平面BCD,∴DE⊥CD,
∵BD⊥CD,BD∩DE=D,
∴CD⊥平面BDE,∵CD?平面CDE,
∴平面BDE⊥平面CDE.
因为BD=CD,且BD⊥CD,BC=2,
所以DM=1,DM⊥BC,AM⊥BC.
又因为平面BCD⊥平面ABC,
所以DM⊥平面ABC,
所以AE∥DM,
又因为AE?平面BCD,DM?平面BCD,
所以AE∥平面BCD.
(Ⅱ)由(Ⅰ)得:AE∥DM,又AE=1,DM=1,
∴四边形DMAE 是平行四边形,
∴DE∥AM,
由(Ⅰ)已证AM⊥BC,又∵平面BCD⊥平面ABC,
∴AM⊥平面BCD,
∴DE⊥平面BCD,
又CD?平面BCD,∴DE⊥CD,
∵BD⊥CD,BD∩DE=D,
∴CD⊥平面BDE,∵CD?平面CDE,
∴平面BDE⊥平面CDE.
点评:本题考查了线面垂直,面面垂直的判定定理,是一道中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
“数列{an}(n∈N*)满足an+1=an•q(其中q为常数)”是“数列{an}(n∈N*)是等比数列”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
下列函数中,周期为π,且在[0,
]上为减函数的是( )
| π |
| 2 |
A、y=sin(2x+
| ||
B、y=cos(2x+
| ||
C、y=sin(x+
| ||
D、y=cos(x+
|
若
=b+i(a,b∈R),其中为虚数单位,则a+b=( )
| a+2i |
| i |
| A、1 | B、2 | C、3 | D、-1 |
函数f(x)=x3+3x-1在以下哪个区间一定有零点( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |