Question

如图，已知平面ABCD⊥平面BCEF，且四边形ABCD为矩形，四边形BCEF为直角梯形，∠CBF=90°，BF∥CE，BC⊥CE，DC=CE=4，BC=BF=2．
（1）作出这个几何体的三视图（不要求写作法）；
（2）设P=DF∩AG，Q是直线DC上的动点，判断并证明直线PQ与直线EF的位置关系；
（3）求三棱锥F-ADE的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,简单空间图形的三视图,空间中直线与直线之间的位置关系

专题：综合题,空间位置关系与距离

分析：（1）利用三视图的作法，作出这个几何体的三视图；
（2）证明EF⊥平面DCF，可得直线PQ与直线EF的位置关系；
（3）利用V_F-ADE=V_E-ADF，求三棱锥F-ADE的体积．

解答： 解：（1）如右图．  
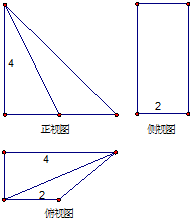
（2）垂直．证明如下：
∵四边形BCEF为直角梯形，∠CBF=90°，BF∥CE，BC⊥CE，BC=BF=2，
∴EF⊥CF，
∵平面ABCD⊥平面BCEF，且四边形ABCD为矩形，
∴DC⊥平面BCEF，
∴DC⊥EF，
∵DC∩CF=C，
∴EF⊥平面DCF，
∵PQ?平面DCF，
∴EF⊥PQ；
（3）∵DC=AB=4，BC=BF=2，
∴AF=2

5

，
设B到平面ADGF的距离为h，则2

5

•h=4×2，
∴h=

4

5

，
∴E到平面ADGF的距离为

4

5

，
∴V_F-ADE=V_E-ADF=

1

3

×

1

2

×2×2

5

×

4

5

=

8

3

．

点评：本题考查线面垂直，考查锥体体积的计算，考查学生分析解决问题的能力，属于中档题．