题目内容
当非空集合S⊆N*,且满足命题“如果x∈S,则8-x∈S”时,回答下列问题.
(1)试写出只有一个元素的集合S;
(2)试写出元素个数为2的S的全部;
(3)满足上述条件的集合S总共有几个.
(1)试写出只有一个元素的集合S;
(2)试写出元素个数为2的S的全部;
(3)满足上述条件的集合S总共有几个.
考点:元素与集合关系的判断
专题:集合
分析:根据已知中S⊆N*,且满足命题“如果x∈S,则8-x∈S”
(1)当S只有一个元素时,x=8-x,解得S;
(2)用列举法,可得到所有元素个数为2的S;
(3)类比n元集合有2n-1个非空真子集,可得满足上述条件的集合S的个数;
(1)当S只有一个元素时,x=8-x,解得S;
(2)用列举法,可得到所有元素个数为2的S;
(3)类比n元集合有2n-1个非空真子集,可得满足上述条件的集合S的个数;
解答:
解:∵S⊆N*,且满足命题“如果x∈S,则8-x∈S”
(1)当S只有一个元素时,x=8-x,
解得:x=4,
故S=4,
(2)当S只有二个元素时,集合S可以为:
{1,7},{2,6},{3,5}
(3)由于集合S中的元素1与7,2与6,3与5必须同时出现,故S中的元素至多有4组,
又∵S≠∅,
故满足条件的S共有24-1=15个
(1)当S只有一个元素时,x=8-x,
解得:x=4,
故S=4,
(2)当S只有二个元素时,集合S可以为:
{1,7},{2,6},{3,5}
(3)由于集合S中的元素1与7,2与6,3与5必须同时出现,故S中的元素至多有4组,
又∵S≠∅,
故满足条件的S共有24-1=15个
点评:本题考查的知识点是元素与集合关系的判断,正确理解条件“如果x∈S,则8-x∈S”是解答的关键.

练习册系列答案
相关题目
 如图,已知平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,∠CBF=90°,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图,已知平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,∠CBF=90°,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2. 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,PD⊥平面ABCD,AB=AD=a,PD=
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,PD⊥平面ABCD,AB=AD=a,PD=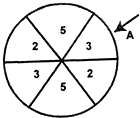 如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).