题目内容
已知在梯形ABCD中,AB∥CD,AB=6,CD=3,E为AB的中点,F为CD上靠近点D的三等分点,且EF⊥AB,EF=2,现将梯形沿着EF翻折,使得平面BCFE⊥平面AEFD,连接BD、BA和CD,如图所示.

(1)求三棱锥E-ABD的体积;
(2)在BD上是否存在一点P,使得CP∥平面AEFD?如果存在,求DP的长;如果不存在,请说明理由.

(1)求三棱锥E-ABD的体积;
(2)在BD上是否存在一点P,使得CP∥平面AEFD?如果存在,求DP的长;如果不存在,请说明理由.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)由VE-ABD=VB-ADE,利用等积法能求出三棱锥E-ABD的体积.
(2)当P为BD上靠近点B的三等分点时,CP∥平面AEFD.连结DE,在DE上取靠近点E的三等分点Q,连结PQ,FQ,
则PQ∥CF,且PQ=CF,四边形PCFQ为平行四边形,由此能求出DP的长.
(2)当P为BD上靠近点B的三等分点时,CP∥平面AEFD.连结DE,在DE上取靠近点E的三等分点Q,连结PQ,FQ,
则PQ∥CF,且PQ=CF,四边形PCFQ为平行四边形,由此能求出DP的长.
解答:
解:(1)由题意得平面BCFE⊥平面AEFD,且平面BCFE∩平面AEFD=FE,
又BE⊥FE,∴BE⊥平面AEFD,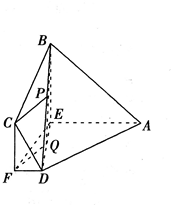
在梯形ABCD中,
由于AB∥CD,AB=6,CD=3,E为AB的中点,
F为CD上靠近点D的三等分点,且EF⊥AB,EF=2,
∴AE=3,DE=
,AD=2
,
由余弦定理,得cos∠ADE=
=
,
则sin∠ADE=
,
∴△ADE面积S=
×DE×AD×sin∠ADE=
×
×2
×
=3,
∴三棱锥E-ABD的体积VE-ABD=VB-ADE=
×3×3=3.
(2)当P为BD上靠近点B的三等分点时,CP∥平面AEFD.
证明如下:
连结DE,在DE上取靠近点E的三等分点Q,连结PQ,FQ,
则PQ∥CF,且PQ=CF,
∴四边形PCFQ为平行四边形,∴CP∥FQ,
∵CP不包含于平面AEFD,FQ?平面AEFD,
∴CP∥平面AEFD,
由(1)知BE⊥平面AEFD,
在Rt△BED中,BD2=BE2+DE2=BE2+EF2+DF2=9+4+1=14,
∴BD=
,DP=
BD=
.
又BE⊥FE,∴BE⊥平面AEFD,

在梯形ABCD中,
由于AB∥CD,AB=6,CD=3,E为AB的中点,
F为CD上靠近点D的三等分点,且EF⊥AB,EF=2,
∴AE=3,DE=
| 5 |
| 2 |
由余弦定理,得cos∠ADE=
| 5+8-9 | ||||
2×2
|
| ||
| 10 |
则sin∠ADE=
3
| ||
| 10 |
∴△ADE面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
3
| ||
| 10 |
∴三棱锥E-ABD的体积VE-ABD=VB-ADE=
| 1 |
| 3 |
(2)当P为BD上靠近点B的三等分点时,CP∥平面AEFD.
证明如下:
连结DE,在DE上取靠近点E的三等分点Q,连结PQ,FQ,
则PQ∥CF,且PQ=CF,
∴四边形PCFQ为平行四边形,∴CP∥FQ,
∵CP不包含于平面AEFD,FQ?平面AEFD,
∴CP∥平面AEFD,
由(1)知BE⊥平面AEFD,
在Rt△BED中,BD2=BE2+DE2=BE2+EF2+DF2=9+4+1=14,
∴BD=
| 14 |
| 2 |
| 3 |
2
| ||
| 3 |
点评:本题考查三棱锥体积的求法,求满足条件的点是否存在的判断与求法,解题时要认真审题,注意空间思想能力的培养.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
化简
-
的结果是( )
| 1-2sin3cos3 |
| 1+2sin3cos3 |
| A、2cos3 |
| B、2sin3 |
| C、-2sin3 |
| D、-2cos3 |
 如图,已知平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,∠CBF=90°,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图,已知平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,∠CBF=90°,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.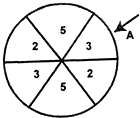 如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).