题目内容
17．公共汽车上有4位乘客，其中任意两人都不在同一车站下车，汽车沿途停靠6个车站，那这4位乘客不同的下车方式共有360种．分析 根据题意，分析可得需要在6个车站中任选4个，安排4人下车，由排列数公式计算可得答案．
解答 解：根据题意，4个人选择6个车站下车，其中任意两人都不在同一车站下车，
则在6个车站中任选4个，安排4人下车即可，
有A64=360种情况，即有360种不同的下车方式，
故答案为：360．
点评 本题考查排列数公式的应用，掌握排列数公式的性质．
练习册系列答案
相关题目
正方体ABCD-A1B1C1D1的棱长为a．E为棱AA1的中点，
2．
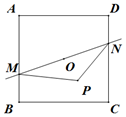正方形ABCD边长为2，中心为O，直线l经过中心O，交AB于M，交CD于N，P为平面上一点，且$2\overrightarrow{OP}=λ\overrightarrow{OB}+（1-λ）\overrightarrow{OC}$，则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是（ ）
正方形ABCD边长为2，中心为O，直线l经过中心O，交AB于M，交CD于N，P为平面上一点，且$2\overrightarrow{OP}=λ\overrightarrow{OB}+（1-λ）\overrightarrow{OC}$，则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是（ ）| A． | $-\frac{3}{4}$ | B． | -1 | C． | $-\frac{7}{4}$ | D． | -2 |
9．已知直线m和不同的平面α，β，下列命题中正确的是（ ）
| A． | $\left.\begin{array}{l}α⊥β\\ m⊥β\end{array}\right\}⇒m∥α$ | B． | $\left.\begin{array}{l}α⊥β\\ m?α\end{array}\right\}⇒m⊥β$ | C． | $\left.\begin{array}{l}m∥α\\ m∥β\end{array}\right\}⇒α∥β$ | D． | $\left.\begin{array}{l}α∥β\\ m?α\end{array}\right\}⇒m∥β$ |
6．已知数列{an}满足${a_1}，\frac{a_2}{a_1}，\frac{a_3}{a_2}，…\frac{a_n}{{{a_{n-1}}}}$是首项为1，公比为2的等比数列，则a101=（ ）
| A． | 2100 | B． | 24950 | C． | 25050 | D． | 25151 |