题目内容
已知椭圆C的中心在原点，焦点在y轴上，焦距为4，且过点，（
，2）求椭圆C的方程．
| 5 |
| 3 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先设焦点在y轴上椭圆的方程，根据已知条件建立方程组，最后通过解方程组，确定椭圆方程．
解答：
解：已知椭圆C的中心在原点，焦点在y轴上，
则：设椭圆的方程为：
+
=1（a＞b＞0）
由于焦距为4
则：a2-b2=4①
点（
，2）在椭圆上
则
+
=1②
所以：由①②得：b2=5 a2=9
故椭圆c的方程为：
+
=1
则：设椭圆的方程为：
| y2 |
| a2 |
| x2 |
| b2 |
由于焦距为4
则：a2-b2=4①
点（
| 5 |
| 3 |
则
| 4 |
| a2 |
| ||
| b2 |
所以：由①②得：b2=5 a2=9
故椭圆c的方程为：
| y2 |
| 9 |
| x2 |
| 5 |
点评：本题考查的知识要点：椭圆标准方程的求法，主要建立a、b、c的关系式，属于基础题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
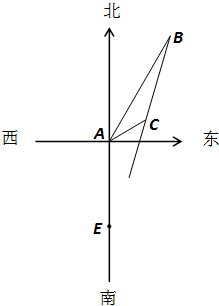在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域．点E正北55海里处有一个雷达观测站A．某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40