题目内容
下列函数中,在区间(0,+∞)上递减的偶函数是( )
| A、y=x3+1 | ||
| B、y=log2(|x|+2) | ||
C、y=(
| ||
| D、y=2|x| |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先确定函数的定义域,再利用函数奇偶性的定义,单调性的定义可得结论.
解答:
解:对于A,定义域为R,函数单调增,是奇函数,不满足题意;
对于B,定义域为R,是偶函数,在(0,+∞)上是增函数,不满足题意;
对于C,定义域为R,是偶函数,在区间(0,+∞)上递减,满足题意;
对于D,定义域为R,是偶函数,在(0,+∞)上是增函数,不满足题意;
故选C.
对于B,定义域为R,是偶函数,在(0,+∞)上是增函数,不满足题意;
对于C,定义域为R,是偶函数,在区间(0,+∞)上递减,满足题意;
对于D,定义域为R,是偶函数,在(0,+∞)上是增函数,不满足题意;
故选C.
点评:本题考查函数单调性与奇偶性的结合,正确运用函数奇偶性、单调性的定义是关键.

练习册系列答案
相关题目
为了解2000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( )
| A、40 | B、50 | C、80 | D、100 |
若关于x的方程|x2-2x-3|-m+5=0有4个根,则m的取值范围为( )
| A、(5,9) |
| B、[5,9] |
| C、(-1,3) |
| D、[-1,3] |
定义在R上的偶函数y=f(x)在[0,+∞)上递减,且f(2)=0,则满足f(log2x)<0的x的集合为( )
A、(
| ||
B、(0,
| ||
C、(-∞,
| ||
D、(
|
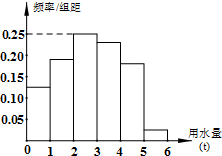 某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表: