题目内容
若关于x的方程|x2-2x-3|-m+5=0有4个根，则m的取值范围为（ ）
| A、（5，9） |
| B、[5，9] |
| C、（-1，3） |
| D、[-1，3] |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由|x2-2x-3|-m+5=0得到|x2-2x-3|=m-5，然后作出函数y=|x2-2x-3|的图象，利用数形结合即可求出m 的取值范围．
解答：
解：由|x2-2x-3|-m+5=0得到|x2-2x-3|=m-5，
作出函数y=|x2-2x-3|的图象，如图：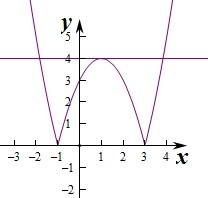
由图象可知要使|x2-2x-3|=m-5，有4个根，
则满足0＜m-5＜4，
即5＜m＜9，
故选A．
作出函数y=|x2-2x-3|的图象，如图：
由图象可知要使|x2-2x-3|=m-5，有4个根，
则满足0＜m-5＜4，
即5＜m＜9，
故选A．
点评：本题主要考查方程根的个数应用断，利用方程和函数之间的关系，转化为两个函数图象的交点问题是解决本题的关键，利用数形结合是解决本题的基本思想．要求熟练掌握二次函数的图象和性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知f（x-1）=x2，则f（x）的解析式为（ ）
| A、f（x）=x2-2x-1 |
| B、f（x）=x2-2x+1 |
| C、f（x）=x2+2x-1 |
| D、f（x）=x2+2x+1 |
下列函数中，在区间（0，+∞）上递减的偶函数是（ ）
| A、y=x3+1 | ||
| B、y=log2（|x|+2） | ||
C、y=(
| ||
| D、y=2|x| |
如图，正六边形ABCDEF的两个顶点A，D为椭圆的两个焦点，其余四个顶点在椭圆上，则该椭圆的离心率为