Question

已知定义在R上的函数f（x）满足：f（x）=

x2+2，x∈[0，1) 2-x2，x∈[-1，0)

且f（x+2）=f（x），g（x）=

2x+5

x+2

，则方程f（x）=g（x）在区间[-5，1]上的所有实根之和为

 

．

Answer 1

考点：分段函数的应用

专题：计算题,数形结合,函数的性质及应用

分析：化简g（x）的表达式，得到g（x）的图象关于点（-2，1）对称，由f（x）的周期性，画出f（x），g（x）的图象，通过图象观察[-5，1]上的交点的横坐标的特点，求出它们的和．

解答： 解：由题意知g(x)=

2x+5

x+2

=

2(x+2)+1

x+2

=2+

1

x+2

，函数f（x）的周期为2，则函数f（x），g（x）在区间[-5，1]上的图象如下图所示：
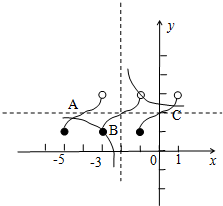由图形可知函数f（x），g（x）在区间[-5，1]上的交点为A，B，C，易知点B的横坐标为-3，若设C的横坐标为t（0＜t＜1），则点A的横坐标为-4-t，所以方程f（x）=g（x）在区间[-5，1]上的所有实数根之和为-3+（-4-t）+t=-7．
故答案为：-7．

点评：本题考查分段函数的图象和运用，考查函数的周期性、对称性和应用，同时考查数形结合的能力，属于中档题．