题目内容
已知抛物线C：y2=4x，F为其焦点，A（3，2），点P是抛物线上的动点，当|PA|+|PF|取得最小值时，P点的坐标是 ．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：确定抛物线焦点F的坐标，由P向准线x=-1作垂线，垂足为M，由抛物线的定义，PF=PM，再由定点A向准线作垂线，垂足为N，利用抛物线的定义，可推断出当且仅当A，P，N三点共线时，|PA|+|PF|取得最小值，答案可得．
解答：
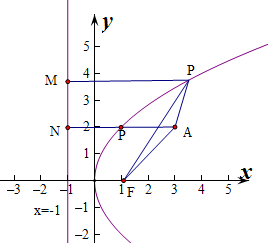解：过P做准线的垂线，则根据抛物线的定义可知焦点F（1，0），准线方程为x=-1，
由抛物线的定义，PF=PM，
再由定点A向准线作垂线，垂足为N，
那么点P在该抛物线上移动时，有|PA+|PF|=|PA|+|PM|≥|AN|，
当且仅当A，P，N三点共线时，取得最小值AN=3-（-1）=4，此时P的纵坐标为2，进而求得横坐标为1．
故|PA|+|PF|取得最小值时P点的坐标是（1，2），
故答案为：（1，2）．
解：过P做准线的垂线，则根据抛物线的定义可知焦点F（1，0），准线方程为x=-1，由抛物线的定义，PF=PM，
再由定点A向准线作垂线，垂足为N，
那么点P在该抛物线上移动时，有|PA+|PF|=|PA|+|PM|≥|AN|，
当且仅当A，P，N三点共线时，取得最小值AN=3-（-1）=4，此时P的纵坐标为2，进而求得横坐标为1．
故|PA|+|PF|取得最小值时P点的坐标是（1，2），
故答案为：（1，2）．
点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，判断A，P，N三点共线时|PA|+|PF|最小，是解题的关键．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
相关题目
已知f（x）=cos2（x-
），若f（α）=p，则f（-α）=q，则下列等式一定成立的是（ ）
| π |
| 4 |
| A、p-q=0 |
| B、p+q=0 |
| C、p+q-1=0 |
| D、p-q+1=0 |