题目内容
已知方程x2-（bcosB）x+acosA=0的两根之积等于两根之和，其中a、b为△ABC的两边，A、B为两内角，试判断三角形形状．
考点：三角形的形状判断
专题：解三角形
分析：利用韦达定理可得bcosB=acosA，再利用正弦定理与二倍角的正弦可得sin2B=sin2A，从而可判断该三角形的形状．
解答：
解：方程x2-（bcosB）x+acosA=0的两根之积等于两根之和，
则bcosB=acosA，又a、b为△ABC的两边，A、B为两内角，
由正弦定理得：sinBcosB=sinAcosA，即sin2B=sin2A，又sin（π-2A）=sin2A，
所以，2B=2A或2B=π-2A，
解得：A=B，或A+B=
．
∴△ABC为等腰三角形或直角三角形．
则bcosB=acosA，又a、b为△ABC的两边，A、B为两内角，
由正弦定理得：sinBcosB=sinAcosA，即sin2B=sin2A，又sin（π-2A）=sin2A，
所以，2B=2A或2B=π-2A，
解得：A=B，或A+B=
| π |
| 2 |
∴△ABC为等腰三角形或直角三角形．
点评：本题考查三角形的形状判断，着重考查正弦定理与二倍角的正弦、诱导公式的应用，属于中档题．
练习册系列答案
相关题目
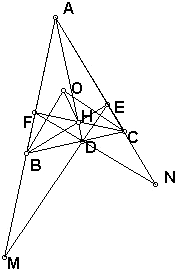如图，△ABC中，O为外心，三条高AD、BE、CF交于点H，直线ED和AB交于点M，FD和AC交于点N．求证：OB⊥DF．
棱长为2的正方体ABCD-A1B1C1D1中，E为C1D1的中点．