题目内容
函数f(x)=|2x-1|,若a<b<c且f(a)>f(c)>f(b),则下列四个式子一成立的是( )
| A、a+c≥0 |
| B、a+c<0 |
| C、b+c≥0 |
| D、b+c<0 |
考点:指数函数的图像与性质
专题:计算题,函数的性质及应用
分析:本题是比较函数值大小的题型,比较方法主要借助函数单调性,由于本题是一个绝对值函数,且三个自变量的具体数值未知,故可以借助函数图象来辅助判断.函数的单调性由图象可以观察出,此也是判断函数单调性的一种方法.
解答:
解:f(x)=
,
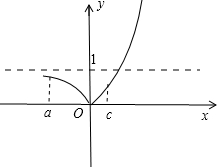
故可作出f(x)=|2x-1|的图象如图所示,
由图可知,要使a<b<c且f(a)>f(c)>f(b)成立,则有a<0且c>0,
且1-2a>2c-1,
∴2a+2c<2.
即2>2a+2c≥2
=2
,
∴2a+c<1,
即a+c<0成立,
故选:B.
|
故可作出f(x)=|2x-1|的图象如图所示,
由图可知,要使a<b<c且f(a)>f(c)>f(b)成立,则有a<0且c>0,
且1-2a>2c-1,
∴2a+2c<2.
即2>2a+2c≥2
| 2a•2c |
| 2a+c |
∴2a+c<1,
即a+c<0成立,
故选:B.

点评:本题主要考查不等式的性质的判断,利用对数函数的性质以及基本不等式是解决本题的关键,综合性较强,难度较大.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
设集合A={x|x2-2x≤0},B={x|-4≤x≤0},则A∩∁RB=( )
| A、R |
| B、{x∈R|X≠0} |
| C、{x|0<x≤2} |
| D、∅ |
设i为虚数单位,则复数
等于( )
| 3-4i |
| i |
| A、4+3i | B、4-3i |
| C、-4+3i | D、-4-3i |
已知某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )


| A、1cm3 |
| B、3cm3 |
| C、5cm3 |
| D、7cm3 |
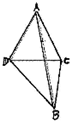 如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?
如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?