题目内容
给定数字0、1、2、3、5、9每个数字最多用一次
(1)可组成多少个四位数?
(2)可组成多少个四位奇数?
(3)可组成多少个四位偶数?
(4)可组成多少个整数?
(1)可组成多少个四位数?
(2)可组成多少个四位奇数?
(3)可组成多少个四位偶数?
(4)可组成多少个整数?
考点:排列、组合的实际应用
专题:计算题,概率与统计
分析:(1)根据题意,运用分步计数原理,依次分析首位数字与后3位数字的情况数目,进而由分步计数原理计算可得答案;
(2)根据题意,运用分步计数原理,先分析末位数字的选法数目,再分析首位数字的选法数目,最后由排列数公式计算第二、三位数字的选法数目,进而由分步计数原理计算可得答案;
(3)在由0、1、2、3、5、9组成的四位数中不是奇数就是偶数,由(1)、(2)的结论,易得答案;
(4)根据题意,依次分析可以组成①一位整数②两位整数③三位整数④四位整数⑤五位整数⑥六位整数的个数,由分类计数原理将其相加即可得答案.
(2)根据题意,运用分步计数原理,先分析末位数字的选法数目,再分析首位数字的选法数目,最后由排列数公式计算第二、三位数字的选法数目,进而由分步计数原理计算可得答案;
(3)在由0、1、2、3、5、9组成的四位数中不是奇数就是偶数,由(1)、(2)的结论,易得答案;
(4)根据题意,依次分析可以组成①一位整数②两位整数③三位整数④四位整数⑤五位整数⑥六位整数的个数,由分类计数原理将其相加即可得答案.
解答:
解:(1)分2步分析:首位数字不能为0,有5个数字可选,即有5种情况,
后3为数字可在剩余5位数字中任选,有A53=60种情况,
故可组成5×60=300个四位数;
(2)分3步分析,
要求是奇数,末位数字必须在1、3、5、9中选取,有4种情况,
首位数字不能为0,有4个数字可选,即有4种情况,
第二、三位数字在剩余的4个数字中选取,有A42=12种情况,
则可以组成4×4×12=192个四位奇数;
(3)由(1)可得,可以组成300个四位数,
由(2)可得,可以组成192个四位奇数,
则可以组成300-192=108个四位偶数,
(4)分6种情况分析:
①、若组成一位数,有0、1、2、3、5、9,共6种情况,即有6个一位数;
②、若组成二位数,十位有5种情况,个位也有5种,则有5×5=25个二位数;
③、若组成三位数,首位不能为0,有5种情况,后2位数字在其余数字中选取,有A52=20种,则可以组成5×20=100个三位数;
④、若组成四位数,首位不能为0,有5种情况,后3位数字在其余数字中选取,有A53=60种,则可以组成5×60=300个四位数;
⑤、若组成五位数,首位不能为0,有5种情况,后4位数字在其余数字中选取,有A54=120种,则可以组成5×120=600个五位数;
⑥、若组成六位数,首位不能为0,有5种情况,后5位数字在其余数字中选取,有A55=120种,则可以组成5×120=600个六位数;
则共有6+100+300+600+600=1631个整数.
后3为数字可在剩余5位数字中任选,有A53=60种情况,
故可组成5×60=300个四位数;
(2)分3步分析,
要求是奇数,末位数字必须在1、3、5、9中选取,有4种情况,
首位数字不能为0,有4个数字可选,即有4种情况,
第二、三位数字在剩余的4个数字中选取,有A42=12种情况,
则可以组成4×4×12=192个四位奇数;
(3)由(1)可得,可以组成300个四位数,
由(2)可得,可以组成192个四位奇数,
则可以组成300-192=108个四位偶数,
(4)分6种情况分析:
①、若组成一位数,有0、1、2、3、5、9,共6种情况,即有6个一位数;
②、若组成二位数,十位有5种情况,个位也有5种,则有5×5=25个二位数;
③、若组成三位数,首位不能为0,有5种情况,后2位数字在其余数字中选取,有A52=20种,则可以组成5×20=100个三位数;
④、若组成四位数,首位不能为0,有5种情况,后3位数字在其余数字中选取,有A53=60种,则可以组成5×60=300个四位数;
⑤、若组成五位数,首位不能为0,有5种情况,后4位数字在其余数字中选取,有A54=120种,则可以组成5×120=600个五位数;
⑥、若组成六位数,首位不能为0,有5种情况,后5位数字在其余数字中选取,有A55=120种,则可以组成5×120=600个六位数;
则共有6+100+300+600+600=1631个整数.
点评:本题主要考查了简单的排列组合在实际问题中的应用,解题时需要注意整数、奇数、偶数的性质,其次需要根据题意,进行合理的分类与分步分析.

练习册系列答案
相关题目
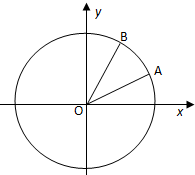 如图,在平面直角坐标系xOy中,以Ox轴为始边,两个锐角α,β的终边分别与单位圆相交于A,B 两点.
如图,在平面直角坐标系xOy中,以Ox轴为始边,两个锐角α,β的终边分别与单位圆相交于A,B 两点.