题目内容
一个物体的运动方程为s=2t2+t+1，其中s的单位是米，t的是秒，那么物体在2秒末的瞬时速度是（ ）
| A、10米/秒 | B、7米/秒 |
| C、9米/秒 | D、8米/秒 |
考点：导数的运算
专题：导数的概念及应用
分析：据对位移求导即得到物体的瞬时速度，求出导函数在t=2时的值，即为物体在2秒末的瞬时速度
解答：
解：求导函数可得s′=4t+1
当t=2时，s′=4t+1=4×2+1=9
故选C．
当t=2时，s′=4t+1=4×2+1=9
故选C．
点评：本题考查导数知识的运用，考查导数的物理意义，属于基础题．
练习册系列答案
高中必刷题系列答案
相关题目
随机变量X的分布列如下，P（1≤X＜4）的值为（ ）
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.2 | 0.3 | x | 0.1 |
| A、0.6 | B、0.7 |
| C、0.8 | D、0.9 |
过双曲线x2-y2=8的左焦点F1有一条弦PQ在左支上，若|PQ|=7，F2是双曲线的右焦点，则△PF2Q的周长是（ ）
| A、28 | ||
B、14-8
| ||
C、14+8
| ||
D、8
|
已知不等式x2-ax+1＞0对任意x∈[0，2]恒成立，则实数a的取值范围为（ ）
A、（-∞，
| ||
| B、（-2，2） | ||
| C、[-2，2] | ||
| D、（-∞，2） |
设n是自然数，f（n）=1+
+
+…+
，经计算可得，f（2）=
，f（4）＞2，f（8）＞
，f（16）＞3，f（32）＞
．观察上述结果，可得出的一般结论是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
A、f（2n）＞
| ||
B、f（n2）≥
| ||
C、f（2n）≥
| ||
D、f(2n)＞
|
正整数按下表的规律排列：则上起第2012行左起2013列的数为（ ）
| A、20122 |
| B、20132 |
| C、2011×2012 |
| D、2012×2013 |
设F1，F2是椭圆
+
=1的左、右两个焦点，若椭圆上满足PF1⊥PF2的点P有且只有两个，则离心率e的值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
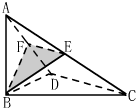如图，△BCD中，∠BCD=90°，AB⊥平面BCD，E，F分别为AC，AD的中点．
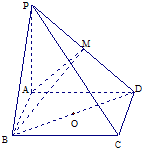如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．BM⊥PD于M．