题目内容
定义:
为n个正数p1,p2,…,pn的“均倒数”,已知数列{an}的前n项的“均倒数”为1+
其中Sn是数列{an}的前n项和,求数列{an}的通项公式及前n项和公式.
| n |
| p1+p2+…+pn |
| an |
| Sn |
考点:数列的求和
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:依题意,可得Sn+an=n,继而知Sn+1+an+1=n+1,两式相减,易知数列{an-1}是以-
为首项,
为公比的等比数列,于是可求得数列{an}的通项公式及前n项和公式.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵
=
=1+
,
∴Sn+an=n,①
Sn+1+an+1=n+1,②
②-①得:2an+1=an+1,即an+1-1=
(an-1),又
=1+
=1+1=2,
∴a1=
,a1-1=-
,
∴数列{an-1}是以-
为首项,
为公比的等比数列,
∴an-1=(-
)•(
)n-1=-(
)n,
∴an=1-(
)n.
设数列{an}的前n项和为Tn,
则Tn=a1+a2+…+an=n-[
+(
)2+…+(
)n]=n-
=n-1+(
)n.
| n |
| a1+a2+…+an |
| n |
| Sn |
| an |
| Sn |
∴Sn+an=n,①
Sn+1+an+1=n+1,②
②-①得:2an+1=an+1,即an+1-1=
| 1 |
| 2 |
| 1 |
| a1 |
| a1 |
| S1 |
∴a1=
| 1 |
| 2 |
| 1 |
| 2 |
∴数列{an-1}是以-
| 1 |
| 2 |
| 1 |
| 2 |
∴an-1=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴an=1-(
| 1 |
| 2 |
设数列{an}的前n项和为Tn,
则Tn=a1+a2+…+an=n-[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
点评:本题考查数列的求和,考查等比关系的确定,求得an=1-(
)n是关键,考查化归思想与推理运算能力,属于中档题.
| 1 |
| 2 |

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积胃( )
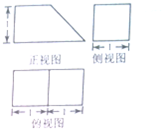

A、1+
| ||||
B、3+
| ||||
C、
| ||||
| D、3 |
矩形ABCD满足AB=2,AD=1,点A、B分别在射线OM,ON上,∠MON为直角,当C到点O的距离最大时,∠BAO的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,ABCD为一个空间四边形,E、F、G、H分别为BD、AB、AC和CD的中点,求证:四边形EFGH为平行四边形.
如图,ABCD为一个空间四边形,E、F、G、H分别为BD、AB、AC和CD的中点,求证:四边形EFGH为平行四边形.