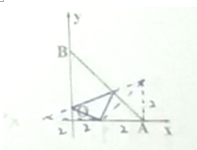
题目内容
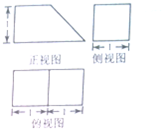
某几何体的三视图如图所示，则该几何体的体积胃（ ）
A、1+
| ||||
B、3+
| ||||
C、
| ||||
| D、3 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图确定该几何体的结构，然后利用相应的体积公式进行求解．
解答：
解：由三视图可知，该几何体是一个底面为直角梯形的四棱柱．
其中棱柱的高为1．
底面直角梯形的上底为1，下底为2，梯形的高为1．
所以四棱柱的体积为V=
×1=
．
故选：C．
其中棱柱的高为1．
底面直角梯形的上底为1，下底为2，梯形的高为1．
所以四棱柱的体积为V=
| (1+2)×1 |
| 2 |
| 3 |
| 2 |
故选：C．
点评：本题主要考查三视图的识别以及几何体的体积公式．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知定义在R上的函数f（x）是奇函数且满足f（
-x）=f（x），f（-2）=-3，若数列{an}的前n项和Sn满足
=
+1，则f（a5）+f（a6）=（ ）
| 3 |
| 2 |
| Sn |
| n |
| 2an |
| n |
| A、-3 | B、-2 | C、2 | D、3 |
数列{an}满足a1=1，a2=2，an+1=2an+1（n≥2），则a21=（ ）
| A、3•220-1 |
| B、3•219-1 |
| C、219-1 |
| D、220-1 |
