题目内容
设y=f(x)(x∈R)对任意实数x1,x2,满足f(x1)+f(x2)=f(x1•x2).求证:
(1)f(1)=f(-1)=0;
(2)f(x)是偶函数.
(1)f(1)=f(-1)=0;
(2)f(x)是偶函数.
考点:抽象函数及其应用,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)可采用赋值法,令x1=x2=1,求得f(1)=0,令x1=x2=-1,求得f(-1)=0,问题得以证明;
(2)可采用赋值法,令x1=-1,x2=x,得到f (-x)=f (-1)+f (x),再令x1=1,x2=-1,求得f(1),同理可求得f(-1),f(x)的奇偶性即可判断.
(2)可采用赋值法,令x1=-1,x2=x,得到f (-x)=f (-1)+f (x),再令x1=1,x2=-1,求得f(1),同理可求得f(-1),f(x)的奇偶性即可判断.
解答:
证明:(1)∵f(x1)+f(x2)=f(x1•x2),
令x1=x2=1,
∴f(1)+f(1)=f(1),
∴f(1)=0,
令x1=x2=-1,
∴f(-1)+f(-1)=f(1),
∴f(-1)=0,
∴f(1)=f(-1)=0;
(2):令x1=1,x2=-1,
则f(1)+f(-1)=f(-1),即f(1)=0,
再令x1=x2=-1得:f(-1)+f(-1)=f(1)=2f(-1)=0,
∴f(-1)=0,
令x1=-1,x2=x,得f(-1)+f(x)=f(-x),
∴f(-x)=f(x),
∴f(x)是偶函数.
令x1=x2=1,
∴f(1)+f(1)=f(1),
∴f(1)=0,
令x1=x2=-1,
∴f(-1)+f(-1)=f(1),
∴f(-1)=0,
∴f(1)=f(-1)=0;
(2):令x1=1,x2=-1,
则f(1)+f(-1)=f(-1),即f(1)=0,
再令x1=x2=-1得:f(-1)+f(-1)=f(1)=2f(-1)=0,
∴f(-1)=0,
令x1=-1,x2=x,得f(-1)+f(x)=f(-x),
∴f(-x)=f(x),
∴f(x)是偶函数.
点评:本题考查函数奇偶性的判断,着重考查学生灵活应用赋值法研究函数的奇偶性,属于中档题.

练习册系列答案
相关题目
对正整数m的3次幂进行如下方式的“分裂”:

仿此规律,若m3的“分裂”中最小的数是211,则m的值是( )

仿此规律,若m3的“分裂”中最小的数是211,则m的值是( )
| A、13 | B、15 | C、17 | D、19 |
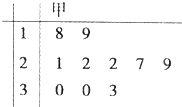 某篮球运动员甲参加了10场比赛,他每场比赛得分的茎叶图如图所示,
某篮球运动员甲参加了10场比赛,他每场比赛得分的茎叶图如图所示,则数据落在区间[22,30)内的概率为( )
| A、0.6 | B、0.5 |
| C、0.4 | D、0.3 |