题目内容
矩形ABCD满足AB=2,AD=1,点A、B分别在射线OM,ON上,∠MON为直角,当C到点O的距离最大时,∠BAO的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:在实际问题中建立三角函数模型
专题:三角函数的求值
分析:如图所示,建立直角坐标系.设∠OAB=θ,则∠CBE=θ.θ∈(0,
).可得B(0,2sinθ),C(sinθ,cosθ+2sinθ).|OC|2=sin2θ+(cosθ+2sinθ)2
=2
sin(2θ-
)+3,由于θ∈(0,
),可得(2θ-
)∈(-
,
).即可得出.
| π |
| 2 |
=2
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
解答:
解:如图所示,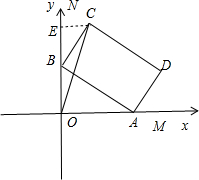
建立直角坐标系.
设∠OAB=θ,则∠CBE=θ.θ∈(0,
).
B(0,2sinθ),C(sinθ,cosθ+2sinθ).
∴|OC|2=sin2θ+(cosθ+2sinθ)2
=1+4sinθcosθ+4sin2θ
=1+2sin2θ+2(1-cos2θ)
=2
sin(2θ-
)+3,
∵θ∈(0,
),∴(2θ-
)∈(-
,
).
∴当2θ-
=
,即θ=
时,|OC|2取得最大值,2
+3.
故选:D.

建立直角坐标系.
设∠OAB=θ,则∠CBE=θ.θ∈(0,
| π |
| 2 |
B(0,2sinθ),C(sinθ,cosθ+2sinθ).
∴|OC|2=sin2θ+(cosθ+2sinθ)2
=1+4sinθcosθ+4sin2θ
=1+2sin2θ+2(1-cos2θ)
=2
| 2 |
| π |
| 4 |
∵θ∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴当2θ-
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| 2 |
故选:D.
点评:本题考查了两点之间的距离公式、点的坐标、两角和差的正弦公式、倍角公式、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
数列{an}满足a1=1,a2=2,an+1=2an+1(n≥2),则a21=( )
| A、3•220-1 |
| B、3•219-1 |
| C、219-1 |
| D、220-1 |