题目内容

解下列不等式：
（1）4x2-20x＜25
（2）-3x2+5x-4＞0．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：将不等式展开，利用一元二次不等式的解法解不等式即可．
解答： 解：（1）∵4x2-20x＜25，
∴4x2-20x-25＜0，
令4x2-20x-25=0
解得x=
20±20
2
8
=
5±
2
2

∴原不等式的解集为（
5-
2
2
，
5+
2
2
），
（2）∵-3x2+5x-4＞0，
∴3x2-5x+4＜0，
∵△=25-4×3×4＜0，
∴原不等式为空集．
点评：本题主要考查一元二次不等式的解法，比较基础．
练习册系列答案
相关题目
设函数f（x）=2sinxcosx-cos（2x-
π
6
）．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的单调递增区间；
（3）当x∈[0，
2π
3
]时，求函数f（x）的最大值及取得最大值时的x的值．
设a＞0，a≠1，函数f（x）=loga|ax2-x|在[3，4]上是增函数，求a的取值范围．
已知0＜x＜1，化简|x|+
(x-1)2
的结果是
 
．
已知f（x）=x5+5x4+10x3+10x2+5x+1，当x=2时用秦九韶算法求v2=
 
．
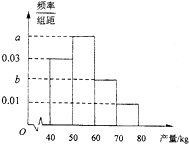果农随机选取某类果树50株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，50]，（50，60]，（60，70]，（70，80]进行分组，得到频率分布直方图如图，已知样本中产量在区间（50，60]上的果树株数是产量在区间（60，80]上的果树株数的
4
3
倍．
（1）求a，b的值；
（2）估计该类果树的平均产量；
（3）为了进一步分析该类果树的情况，现要用分层抽样的方法，从中再抽取20株，那么在（60，70]区间内应抽取多少株？
已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=2x-3•2-x．
（1）求函数f（x）的解析式；
（2）求方程f（x）=
1
2
的负数解．
给出下列结论：
①命题“?x∈R，sinx≠1”的否定是“?x∈R，sinx=1”；
②命题“有些正方形是平行四边形”的否定是“所有正方形不都是平行四边形”；
③命题“A1，A2是对立事件”是命题“A1，A2是互斥事件”的充分不必要条件；
④若a，b是实数，则“a+b＞0且ab＞0”是“a＞0且b＞0”的必要不充分条件．
其中正确结论的是
 
．
求函数y=log0.5（1-3x）-log2（3x+
1
3
）的最小值，并求出相应的x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网