题目内容
20.已知函数f(x)满足f(x3-1)=$\frac{lnx}{{x}^{2}}$,求f′(x).分析 利用换元法,求出函数的解析式,再根据导数的运算法则求导即可.
解答 解:设x3-1=t,则x=$\root{3}{1+t}$,
∵x>0,则t>-1,
∴f(t)=$\frac{ln\root{3}{1+t}}{\root{3}{(1+t)^{2}}}$=$\frac{1}{3}$(1+t)${\;}^{-\frac{2}{3}}$ln(1+t),
∴f(x)=$\frac{1}{3}$(1+x)${\;}^{-\frac{2}{3}}$ln(1+x),
∴f′(x)=$\frac{1}{3}$[-$\frac{2}{3}$$(1+x)^{-\frac{5}{3}}$$•\frac{1}{1+x}$]=-$\frac{2}{9}$$(1+x)^{-\frac{8}{3}}$.
点评 本题考查了函数解析式的求法和导数的运算法则,属于基础题.

练习册系列答案
相关题目
11.$\root{3}{x\sqrt{x}}$的结果为( )
| A. | x${\;}^{\frac{1}{2}}$ | B. | x${\;}^{\frac{9}{2}}$ | C. | x${\;}^{\frac{3}{2}}$ | D. | x${\;}^{\frac{2}{3}}$ |
19.设抛物线x2=4y的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的倾斜角等于30°,那么|$\overrightarrow{PF}$|等于( )
| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
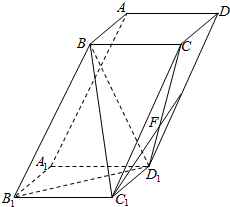 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.