题目内容
已知实数x,y满足
,则
的取值范围是( )
|
| y-6 |
| x-5 |
| A、[2,3] | ||||
| B、[1,2] | ||||
C、[
| ||||
D、[
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用k的几何意义,利用数形结合即可得到结论.
解答:
解:设k=
,则k的几何意义为动点P(x,y),到定点C(5,6)的斜率,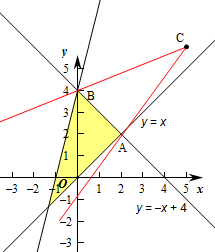
作出不等式组对应的平面区域如图:
由图象可知,BC的斜率最小,AC的斜率最大,
其中B(0,4),此时BC的斜率k=
=
,
由
,解得
,即A(2,2),
此时AC的斜率k=
=
,
故k∈[
,
],
故选:D
| y-6 |
| x-5 |

作出不等式组对应的平面区域如图:
由图象可知,BC的斜率最小,AC的斜率最大,
其中B(0,4),此时BC的斜率k=
| 4-6 |
| 0-5 |
| 2 |
| 3 |
由
|
|
此时AC的斜率k=
| 2-6 |
| 2-5 |
| 4 |
| 3 |
故k∈[
| 2 |
| 5 |
| 4 |
| 3 |
故选:D
点评:本题主要考查线性规划的应用,利用数形结合是解决此类问题的基本方法,利用k的几何意义是解决本题的关键.

练习册系列答案
相关题目
若
,
是两个单位向量,则下列结论正确的是( )
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、|
|
函数f(x)=x2-2ax-3在区间(-8,2)上为减函数,则有( )
| A、a∈(-∞,1] |
| B、a∈[2,+∞) |
| C、a∈[1,2] |
| D、a∈(-∞,1]∪[2,+∞) |
设x0是方程lnx+x=4的解,则x0在下列哪个区间内( )
| A、(3,4) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
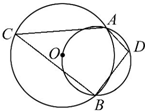 如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为( )
如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为( )| A、35° | B、40° |
| C、50° | D、80° |
已知集合A={x|x2+x-2<0},集合B={x|-2<x<3},则∁BA等于( )
| A、{x|1≤x<3} |
| B、{x|2≤x<3} |
| C、{x|-2<x<1} |
| D、{x|-2<x≤-1或2≤x<3} |
在平面直角坐标系中,设M(-3,2)、N(2,-3),沿x轴把坐标平面折成90°的二面角后,则|
|的长为( )
| MN |
A、
| ||
B、
| ||
C、2
| ||
D、5
|
 如图,已知双曲线的中心在坐标原点O,左焦点为F,C是双曲线虚轴的下顶点,双曲线的一条渐近线OD与直线FC相交于点D,若双曲线的离心率为2,则∠ODF的余弦值是( )
如图,已知双曲线的中心在坐标原点O,左焦点为F,C是双曲线虚轴的下顶点,双曲线的一条渐近线OD与直线FC相交于点D,若双曲线的离心率为2,则∠ODF的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
计算
2xdx=( )
| ∫ | 2 1 |
| A、3 | B、-3 | C、-4 | D、4 |