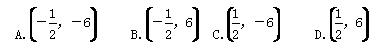题目内容
设函数f(x)=ex(sin x-cos x)(0≤x≤2 012π),则函数f(x)的各极小值之和为( )

D
[解析] f′(x)=(ex)′(sin x-cos x)+ex(sin x-cos x)′=2exsin x,若f′(x)<0,则x∈(π+2kπ,2π+2kπ),k∈Z;若f′(x)>0,则x∈(2kπ,π+2kπ),k∈Z.所以当x=2π+2kπ,k∈Z时,f(x)取得极小值,其极小值为f(2π+2kπ)=e2kπ+2π[sin(2π+2kπ)-cos(2π+2kπ)]=e2kπ+2π×(0-1)=-e2kπ+2π,k∈Z.因为0≤x≤2 012π,又在两个端点的函数值不是极小值,所以k∈[0,1 004],所以函数f(x)的各极小值构成以-e2π为首项,以e2π为公比的等比数列,共有1 005项,故函数f(x)的各极小值之和为S1 005=-e2π-e4π-…-e2 010π=-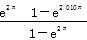 ,故选D.
,故选D.

练习册系列答案
相关题目
 的实数解落在的区间是 ( )
的实数解落在的区间是 ( )



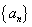 是等差数列,其前
是等差数列,其前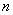 项和为
项和为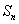 ,
,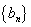 是等比数列,且
是等比数列,且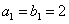 ,
,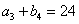 ,
,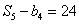 .
.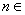 N
N ,是否存在正实数
,是否存在正实数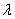 ,使不等式
,使不等式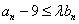 恒成立,若存在,求出
恒成立,若存在,求出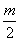 g(x0)成立?如果存在,求出符合条件的一个x0;否则说明理由.
g(x0)成立?如果存在,求出符合条件的一个x0;否则说明理由. ,其前n项积为Tn,则T2 014=( )
,其前n项积为Tn,则T2 014=( )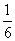 B.-
B.-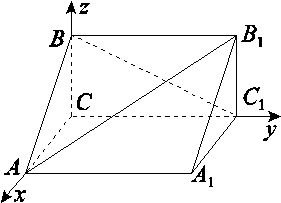
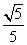 B.
B.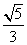 C.
C.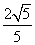 D.
D.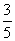
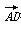 =(2,8),
=(2,8),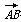 =(-3,4),对角线AC与BD相交于点M,则
=(-3,4),对角线AC与BD相交于点M,则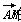 的坐标为( )
的坐标为( )