题目内容
若x∈[-2,2]时,x2-2x+2≥t2恒成立,求实数t的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:设f(x)=x2-2x+2,然后求函数f(x)的最小值即可.
解答:
解:因为x2-2x+2≥t2,设f(x)=x2-2x+2,
要使不等式恒成立,则只需求出函数f(x)在[-2,2]上的最小值f(x)min,使f(x)min≥t2即可.
因为f(x)=x2-2x+2=(x-1)2+1,对称轴为x=1,
因为-2≤x≤2,所以当x=1时,函数取得最小值为1,
由1≥t2,解得-1≤t≤1,
实数t的取值范围[-1,1].
要使不等式恒成立,则只需求出函数f(x)在[-2,2]上的最小值f(x)min,使f(x)min≥t2即可.
因为f(x)=x2-2x+2=(x-1)2+1,对称轴为x=1,
因为-2≤x≤2,所以当x=1时,函数取得最小值为1,
由1≥t2,解得-1≤t≤1,
实数t的取值范围[-1,1].
点评:本题主要考查不等式恒成立问题,将恒成立问题转化为最值横成立,利用函数的最值求参数的范围是解决本题的关键.

练习册系列答案
相关题目
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x•f(x)>0的解集是( )
| A、{x|-3<x<0,或x>3} |
| B、{x|x<-3,或0<x<3} |
| C、{x|x<-3,或x>3} |
| D、{x|-3<x<0,或0<x<3} |
用an表示正整数n的最大奇因数(如a3=3、a10=5),记数列{an}的前n项的和为Sn,则S64值为( )
| A、342 | B、1366 |
| C、2014 | D、5462 |
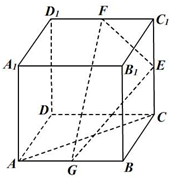 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.