题目内容
将边长为1的正方形ABCD沿对角线BD折成直二面角,则二面角B-AC-D的余弦值为 .
考点:与二面角有关的立体几何综合题
专题:综合题,空间角
分析:取BD的中点E,连接CE,取AC的中点F,连接BF,DF,则BF⊥AC,DF⊥AC,可得∠BFD为二面角B-AC-D的平面角,求出三角形的三边,利用余弦定理,可求二面角B-AC-D的余弦值.
解答:
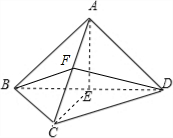 解:取BD的中点E,连接CE,则AE⊥BD,
解:取BD的中点E,连接CE,则AE⊥BD,
∵平面ABD∩平面BCD=BD,平面ABD⊥平面BCD
∴AE⊥平面BCD
∵正方形ABCD的边长为1,
∴AE=CE=
,
∴AC=1,
取AC的中点F,连接BF,DF,则BF⊥AC,DF⊥AC.
∴∠BFD为二面角B-AC-D的平面角.
∵AB=BC=DA=DC=1,
∴BF=DF=
,
∵BD=
,
∴cos∠BFD=
=-
.
∴二面角B-AC-D的余弦值为-
.
故答案为:-
.
 解:取BD的中点E,连接CE,则AE⊥BD,
解:取BD的中点E,连接CE,则AE⊥BD,∵平面ABD∩平面BCD=BD,平面ABD⊥平面BCD
∴AE⊥平面BCD
∵正方形ABCD的边长为1,
∴AE=CE=
| ||
| 2 |
∴AC=1,
取AC的中点F,连接BF,DF,则BF⊥AC,DF⊥AC.
∴∠BFD为二面角B-AC-D的平面角.
∵AB=BC=DA=DC=1,
∴BF=DF=
| ||
| 2 |
∵BD=
| 2 |
∴cos∠BFD=
| ||||||||
2•
|
| 1 |
| 3 |
∴二面角B-AC-D的余弦值为-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题考查图形的翻折,考查面面角,考查余弦定理的运用,正确作出面面角是关键.

练习册系列答案
相关题目
若对于任意的正数x,不等式3x(x2-2a)>1恒成立,则a的取值范围是( )
| A、(-∞,+∞) | ||
| B、(-2,+∞) | ||
C、(
| ||
D、(-∞,-
|