题目内容
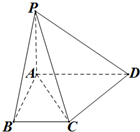
在二面角α-l-β 的半平面α内，线段AB⊥l，垂足为B；在半平面β内，线段CD⊥l，垂足为D；M为l上任一点．若AB=2，CD=3，BD=1，则AM+CM的最小值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：多面体和旋转体表面上的最短距离问题,与二面角有关的立体几何综合题
专题：空间位置关系与距离
分析：设BM=x，则DM=1-x，AM+BM=
+
，由此能求出AM+BM取最小值．
| x2+4 |
| (x-1)2+9 |
解答：
解：设BM=x，则DM=1-x，
∵AB=2，CD=3，BD=1，
∴AM+BM=
+
，
建立平面直角坐标系，
AM+BM可以看作动点P（x，0）到两定点S（0，2），Q（1，-3）的距离之和，
当点P在线段PS上时，
AM+BM取最小值，最小值为线段SQ的长，
∴（AM+BM）min=|SQ|=
=
．
故选：A．
∵AB=2，CD=3，BD=1，
∴AM+BM=
| x2+4 |
| (x-1)2+9 |
建立平面直角坐标系，
AM+BM可以看作动点P（x，0）到两定点S（0，2），Q（1，-3）的距离之和，
当点P在线段PS上时，
AM+BM取最小值，最小值为线段SQ的长，
∴（AM+BM）min=|SQ|=
| 12+(-3-2)2 |
| 26 |
故选：A．
点评：本题也可以将二面角展平成一个平面，这样只须求出在“平面”内，A、C两点之间的距离即为AM+BM的最小值．
练习册系列答案
相关题目
设x=log52，y=e-
，z=
（e是自然对数的底数），则（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、x＜y＜z |
| B、y＜x＜z |
| C、z＜x＜y |
| D、x＜z＜y |
定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2]时，f(x)=
，若x∈[-2，0]时，f(x)≥
-
恒成立，则实数t的取值范围是（ ）
|
| t |
| 2 |
| 1 |
| t |
| A、[-2，0）∪（0，1） |
| B、[-2，0）∪[1，+∞） |
| C、[-2，1] |
| D、（-∞，-2]∪（0，1] |
若对于任意的正数x，不等式3x（x2-2a）＞1恒成立，则a的取值范围是（ ）
| A、（-∞，+∞） | ||
| B、（-2，+∞） | ||
C、（
| ||
D、（-∞，-
|
已知A，B，C是单位圆O上任意的不同三点，若
=2
+x
，则正实数x的取值范围为（ ）
| OA |
| OB |
| OC |
| A、（0，2] |
| B、[1，3] |
| C、[2，4] |
| D、[3，5] |
如图，直角梯形ABCD中，∠ABC=∠BAD=90°，