题目内容
9.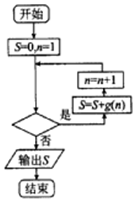 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2014? | B. | n≤2015? | C. | n>2014? | D. | n>2015? |
分析 根据已知中的程序框图可得,该程序的功能是计算并输出变量S的值,模拟程序的运行过程,可得答案.
解答 解:函数f(x)=ax3+$\frac{1}{2}$x2,在x=-1处取得极大值,
即f′(x)=3ax2+x的零点为-1,
即 3a-a=0,解得:a=$\frac{1}{3}$,
故f′(x)=x2+x,
故g(x)=$\frac{1}{f′(x)}$=$\frac{1}{x}$-$\frac{1}{x+1}$,
则S=g(1)+g(2)+g(3)+…+g(k)=1-$\frac{1}{k+1}$=$\frac{k}{k+1}$,
若输出的结果S>$\frac{2014}{2015}$,则k>2015,
故进行循环的条件应为n≤2015?,
故选:B.
点评 本题以程序框图为载体,考查了函数在某点取得极值的条件,数列求和,难度中档.

练习册系列答案
相关题目
1.直线x+2y-1=0在y轴上的截距为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | 1 |
1.设x∈R,记不超过x的最大整数为[x],如[0.9]=0,[2.6]=2,令{x}=x-[x].则{$\frac{\sqrt{5}+1}{2}$},[$\frac{\sqrt{5}+1}{2}$],$\frac{\sqrt{5}+1}{2}$( )
| A. | 既是等差数列又是等比数列 | B. | 既不是等差数列也不是等比数列 | ||
| C. | 是等差数列但不是等比数列 | D. | 是等比数列但不是等差数列 |
19.下列每组函数是同一函数的是( )
| A. | f(x)=x0与f(x)=1 | B. | f(x)=$\sqrt{{x}^{2}}$-1与f(x)=|x|-1 | ||
| C. | f(x)=$\frac{{x}^{2}-4}{x+2}$与f(x)=x-2 | D. | f(x)=$\sqrt{(x-1)(x-2)}$与f(x)=$\sqrt{x-1}$$\sqrt{x-2}$ |