题目内容
19.下列每组函数是同一函数的是( )| A. | f(x)=x0与f(x)=1 | B. | f(x)=$\sqrt{{x}^{2}}$-1与f(x)=|x|-1 | ||
| C. | f(x)=$\frac{{x}^{2}-4}{x+2}$与f(x)=x-2 | D. | f(x)=$\sqrt{(x-1)(x-2)}$与f(x)=$\sqrt{x-1}$$\sqrt{x-2}$ |
分析 根据两个函数的定义域相同,对应关系也相同,判断它们是同一函数即可.
解答 解:对于A:f(x)=x0的定义域为{x|x≠0},而f(x)=1的定义域为R,定义域不同,∴不是同一函数;
对于B:f(x)=$\sqrt{{x}^{2}}$-1=|x|-1,的定义域为R,而f(x)=|x|-1的定义域为R,它们定义域相同,对应关系也相同,∴是同一函数;
对于C:f(x)=$\frac{{x}^{2}-4}{x+2}$的定义域为{x|x≠-2},而与f(x)=x-2的定义域为R,定义域不同,∴不是同一函数;
对于D:f(x)=$\sqrt{(x-1)(x-2)}$的定义域为{x|x≥2或x≤1},而f(x)=$\sqrt{x-1}$$\sqrt{x-2}$的定义域为{x|x≥2},定义域不同,∴不是同一函数;
故选B.
点评 本题考查了判断两个函数是否为同一函数的问题,是基础题目.

练习册系列答案
相关题目
9.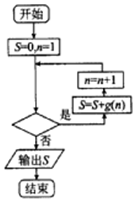 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2014? | B. | n≤2015? | C. | n>2014? | D. | n>2015? |
10.已知不等式x2-2ax+a>0(x∈R)恒成立,则不等式a2x+1<a${\;}^{{x}^{2}+2x-3}$<1的解集是( )
| A. | (1,2) | B. | (-$\frac{1}{2}$,2) | C. | (-2,2) | D. | (-3,2) |
7.设Sn是等差数列{an}的前n项和,若$\frac{a_8}{a_7}=\frac{13}{5}$,则$\frac{{{S_{15}}}}{{{S_{13}}}}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.已知幂函数f ( x )过点(2,$\sqrt{2}$),则f ( 9 )的值为( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | 3 | D. | 6 |
9.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了了解该单位职工的健康情况,决定采用分层抽样的方法,从中抽取容量为15的样本.则从上述各层中依次抽取的人数分别是( )
| A. | 8,4,3 | B. | 6,5,4 | C. | 7,5,3 | D. | 8,5,2 |
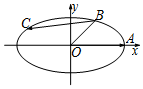 如图,椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右顶点,B是该椭圆在第一象限部分上的一点,且∠AOB=$\frac{π}{4}$.若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为[-9,3].
如图,椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右顶点,B是该椭圆在第一象限部分上的一点,且∠AOB=$\frac{π}{4}$.若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为[-9,3].