题目内容
3.已知tanα=-3,且α是第二象限的角.(1)求cosα的值;
(2)求$\frac{4sinα-2cosα}{5cosα+3sinα}$的值.
分析 (1)由已知利用同角三角函数基本关系式可求sinα=-3cosα,联立sin2α+cos2α=1,结合α是第二象限的角,即可解得cosα的值;
(2)利用同角三角函数基本关系式化简所求即可计算得解.
解答 解:(1)因为tanα=-3,且α是第二象限的角,
∴$tanα=\frac{sinα}{cosα}=-3$,
∴sinα=-3cosα.…(2分)
∵sin2α+cos2α=1,…(4分)
∵cosα<0,
∴$cosα=-\frac{{\sqrt{10}}}{10}$,…(8分)
$sinα=\sqrt{1-{{cos}^2}α}=\frac{{3\sqrt{10}}}{10}$.…(10分)
(2)因为tanα=-3
∴原式=$\frac{{(4sinα-2cosα)×\frac{1}{cosα}}}{{(5cosα+3sinα)×\frac{1}{cosα}}}$=$\frac{4tanα-2}{5+3tanα}$=$\frac{4×(-3)-2}{5+3×(-3)}$=$\frac{7}{2}$.…(12分)
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.设P={x|x>4},Q={x|-2<x<2},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P?∁RQ | D. | Q⊆∁RP |
11.已知a、b 是实数,则“a>b”是“a2>b2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
8.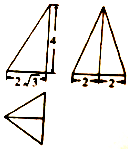 若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
 若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )| A. | 34π | B. | $\frac{80π}{3}$ | C. | $\frac{91}{3}π$ | D. | 114π |
15.设当x=θ时,函数f(x)=3sinx+4cosx取得最小值,则sinθ=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
9.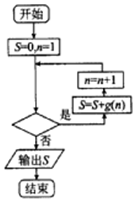 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2014? | B. | n≤2015? | C. | n>2014? | D. | n>2015? |