��Ŀ����
1����x��R���Dz�����x���������Ϊ[x]����[0.9]=0��[2.6]=2����{x}=x-[x]����{$\frac{\sqrt{5}+1}{2}$}��[$\frac{\sqrt{5}+1}{2}$]��$\frac{\sqrt{5}+1}{2}$��������| A�� | ���ǵȲ��������ǵȱ����� | B�� | �Ȳ��ǵȲ�����Ҳ���ǵȱ����� | ||
| C�� | �ǵȲ����е����ǵȱ����� | D�� | �ǵȱ����е����ǵȲ����� |
���� ���¶��廯��{$\frac{\sqrt{5}+1}{2}$}��[$\frac{\sqrt{5}+1}{2}$]��Ȼ���ϵȲ����к͵ȱ����еĸ����жϣ�
��� �⣺������ɵ�{$\frac{\sqrt{5}+1}{2}$}=$\frac{\sqrt{5}+1}{2}-1=\frac{\sqrt{5}-1}{2}$��[$\frac{\sqrt{5}+1}{2}$]=1��
��${1}^{2}=\frac{\sqrt{5}-1}{2}��\frac{\sqrt{5}+1}{2}$��
��$\frac{\sqrt{5}-1}{2}��1��\frac{\sqrt{5}+1}{2}$���ɵȱ����У�
��$\frac{\sqrt{5}-1}{2}+\frac{\sqrt{5}+1}{2}��2$��
��{$\frac{\sqrt{5}+1}{2}$}��[$\frac{\sqrt{5}+1}{2}$]��$\frac{\sqrt{5}+1}{2}$�ǵȱ����е����ǵȲ����У�
��ѡ��D��
���� ���⿼��Ȳ����к͵ȱ����еĸ���ǻ����ļ����⣮

��ϰ��ϵ�д�
 ������������ϵ�д�
������������ϵ�д�
�����Ŀ
15���赱x=��ʱ������f��x��=3sinx+4cosxȡ����Сֵ����sin��=��������
| A�� | $\frac{3}{5}$ | B�� | $\frac{4}{5}$ | C�� | $-\frac{3}{5}$ | D�� | $-\frac{4}{5}$ |
9��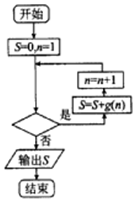 ��֪����f��x��=ax3+$\frac{1}{2}$x2��x=-1��ȡ�ü���ֵ����g��x��=$\frac{1}{f�䣨x��}$�������ͼ��ͼ��ʾ��������Ľ��S��$\frac{2014}{2015}$�����жϿ��п�������Ĺ���n���ж������ǣ�������
��֪����f��x��=ax3+$\frac{1}{2}$x2��x=-1��ȡ�ü���ֵ����g��x��=$\frac{1}{f�䣨x��}$�������ͼ��ͼ��ʾ��������Ľ��S��$\frac{2014}{2015}$�����жϿ��п�������Ĺ���n���ж������ǣ�������
 ��֪����f��x��=ax3+$\frac{1}{2}$x2��x=-1��ȡ�ü���ֵ����g��x��=$\frac{1}{f�䣨x��}$�������ͼ��ͼ��ʾ��������Ľ��S��$\frac{2014}{2015}$�����жϿ��п�������Ĺ���n���ж������ǣ�������
��֪����f��x��=ax3+$\frac{1}{2}$x2��x=-1��ȡ�ü���ֵ����g��x��=$\frac{1}{f�䣨x��}$�������ͼ��ͼ��ʾ��������Ľ��S��$\frac{2014}{2015}$�����жϿ��п�������Ĺ���n���ж������ǣ�������| A�� | n��2014�� | B�� | n��2015�� | C�� | n��2014�� | D�� | n��2015�� |
10����֪����ʽx2-2ax+a��0��x��R�����������ʽa2x+1��a${\;}^{{x}^{2}+2x-3}$��1�Ľ⼯�ǣ�������
| A�� | ��1��2�� | B�� | ��-$\frac{1}{2}$��2�� | C�� | ��-2��2�� | D�� | ��-3��2�� |
11����֪�ݺ���f �� x �����㣨2��$\sqrt{2}$������f �� 9 ����ֵΪ��������
| A�� | $\frac{1}{3}$ | B�� | 1 | C�� | 3 | D�� | 6 |
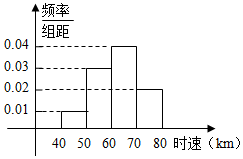 ��֪200������ͨ��ijһ�ι�·ʱ��ʱ�ٵ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
��֪200������ͨ��ijһ�ι�·ʱ��ʱ�ٵ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��