题目内容
已知函数f（x）=
，则函数g（x）=f（x）-e-x的零点个数是（ ）
|
| A、4 | B、3 | C、2 | D、1 |
考点：根的存在性及根的个数判断,函数零点的判定定理
专题：函数的性质及应用
分析：由g（x）=0，利用方程和函数之间的关系，转化为函数f（x）和y=e-x，的交点个数问题，即可得到结论．
解答：
解：由g（x）=0，得f（x）=e-x，
分别作出函数f（x）和y=e-x，的图象如图：
由图象可知，两个图象的交点个数为2个，
即函数g（x）的零点个数为2个，
故选：C
分别作出函数f（x）和y=e-x，的图象如图：
由图象可知，两个图象的交点个数为2个，
即函数g（x）的零点个数为2个，
故选：C
点评：本题主要考查函数零点个数的判定，将方程转化为两个函数的相交个数问题是解决本题问题的基本方法．
练习册系列答案
相关题目
已知α∈（
，π），且cosα=-
，则sinα=（ ）
| π |
| 2 |
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
如图是一组样本数据的频率分布直方图，则依据图形中的数据，可以估计总体的平均数与中位数分别是（ ）| A、12.5 12.5 |
| B、13 13 |
| C、13.5 12.5 |
| D、13.5 13 |
命题p：
≤0；命题q：y=xa（x为自变量）在第一象限是增函数，则p是q的（ ）
| a |
| a-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设奇函数f（x）=cos（ωx+φ）-
sin（ωx+φ）（ω＞0，|φ|＜
）的最小正周期为π，则ω，φ分别是（ ）
| 3 |
| π |
| 2 |
A、2，
| ||||
B、
| ||||
C、
| ||||
D、2，
|
某校高二年级文科共303名学生，为了调查情况，学校决定随机抽取50人参加抽测，采取先简单随机抽样去掉3人然后系统抽样抽取出50人的方式进行．则在此抽样方式下，某学生甲被抽中的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
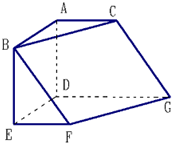在图的几何体中，面ABC∥面DEFG，∠BAC=∠EDG=120°，四边形ABED是矩形，四边形ADGC是直角梯形，∠ADG=90°，四边形DEFG是梯形，EF∥DG，AB=AC=AD=EF=1，DG=2．