题目内容
已知函数f(x)=loga(1-ax),其中a>0,a≠1.
(1)求反函数f-1(x)及其定义域;
(2)解关于x的不等式loga(1-ax)>f-1(1).
(1)求反函数f-1(x)及其定义域;
(2)解关于x的不等式loga(1-ax)>f-1(1).
考点:反函数,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)由已知得ax=1-ay,从而x=loga(1-ay),由此能求出反函数f-1(x)=loga(1-ax),a>0,a≠1.
当0<a<1时,1-ax>0,则x>0即定义域为(0,+∞);当a>1时,1-ax>0,则x<0,则定义域为(-∞,0).
(2)由已知得loga(1-ax)>f-1(1)=loga(1-a),当0<a<1时,解得x∈(0,1);当a>1时,解得x∈(-∞,0).
当0<a<1时,1-ax>0,则x>0即定义域为(0,+∞);当a>1时,1-ax>0,则x<0,则定义域为(-∞,0).
(2)由已知得loga(1-ax)>f-1(1)=loga(1-a),当0<a<1时,解得x∈(0,1);当a>1时,解得x∈(-∞,0).
解答:
解:(1)∵f(x)=y=loga(1-ax),其中a>0,a≠1,
∴ay=1-ax,
∴ax=1-ay,
x=loga(1-ay),
x,y互换,得反函数f-1(x)=loga(1-ax),a>0,a≠1.
当0<a<1时,1-ax>0,则x>0即定义域为(0,+∞);
当a>1时,1-ax>0,则x<0,则定义域为(-∞,0);
(2)∵f-1(1)=loga(1-a),
∴loga(1-ax)>f-1(1)=loga(1-a),
当0<a<1时,1-ax<1-a,
解得x∈(0,1);
当a>1时,1-ax>1-a,
解得x∈(-∞,0).
∴ay=1-ax,
∴ax=1-ay,
x=loga(1-ay),
x,y互换,得反函数f-1(x)=loga(1-ax),a>0,a≠1.
当0<a<1时,1-ax>0,则x>0即定义域为(0,+∞);
当a>1时,1-ax>0,则x<0,则定义域为(-∞,0);
(2)∵f-1(1)=loga(1-a),
∴loga(1-ax)>f-1(1)=loga(1-a),
当0<a<1时,1-ax<1-a,
解得x∈(0,1);
当a>1时,1-ax>1-a,
解得x∈(-∞,0).
点评:本题考查函数的反函数及其定义域的求法,考查关于x的不等式的解法,解题时要认真审题,是中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
对于实数x,y满足命题p:x+y≠8,命题q:x≠2或y≠6,则命题p是命题q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
an=
时,数列{an}的最小项是( )
n-
| ||
n-
|
| A、a1 |
| B、a44 |
| C、a45 |
| D、a50 |
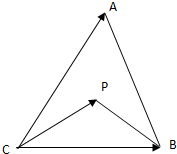 如图示,已知A、B、C为平面上的三个定点,∠ACB=60°,动点P在∠ACB的平分线上,记
如图示,已知A、B、C为平面上的三个定点,∠ACB=60°,动点P在∠ACB的平分线上,记