题目内容

7．如图，在△ABC中，AD⊥AB，BC=2BD，AD=1，则$\overrightarrow{AD}•\overrightarrow{AC}+\overrightarrow{AD}•\overrightarrow{BC}$=（　　）
A．8B．4C．2D．1

分析 以AD，AB为坐标轴建立平面直角坐标系，设AB=a，用a表示出$\overrightarrow{AC}$，$\overrightarrow{BC}$，代入向量的数量积公式计算．

解答 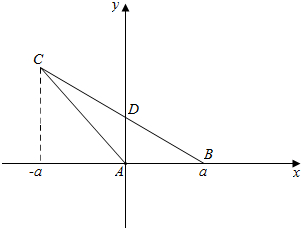解：以AD，AB为坐标轴建立平面直角坐标系，设AB=a，则A（0，0），B（a，0），D（0，1），
∵BC=2BD，∴C（-a，2）．∴$\overrightarrow{AD}$=（0，1），$\overrightarrow{AC}$=（-a，2），$\overrightarrow{BC}$=（-2a，2），
∴$\overrightarrow{AD}•\overrightarrow{AC}+\overrightarrow{AD}•\overrightarrow{BC}$=2+2=4．
故选：B．

点评 本题考查了平面向量的数量积运算，属于基础题．

练习册系列答案
相关题目
1．下列求导运算中正确的是（　　）
A．（x+$\frac{1}{x}$）′=1+$\frac{1}{{x}^{2}}$B．（lgx）′=$\frac{1}{xln10}$C．（lnx）′=xD．（x2cosx）′=-2xsinx
15．已知全集U=R，集合A={x∈N|y=$\sqrt{4-x}$}，B={y|y=2x-1}，则A∩B=（　　）
A．{x|0≤x≤4}B．{1，2，3，4}C．{0，1，2，3，4}D．{0，1，2，3}
12．若m∈A，则m+1∈A，m-1∈A．那么满足条件的集合A可能为（　　）
A．{y|y=cos（2x+1）}B．{y|y=$\frac{x-1}{x+1}$}C．{y|y=lg（x2-1）}D．{y|y=2x+2-x）}
2．判断下列对应是否是实数集R上的函数：
（1）f：把x对应到3x+1；
（2）g：把x对应到|x|+1；
（3）h：把x对应到$\frac{1}{2x-5}$；
（4）r：把x对应到$\sqrt{3x+6}$．
12．定积分$\int_{-2}^2{（\sqrt{4-{x^2}}+|x|）dx}$=2π+4．
19．复数z满足“（|z|-2i）（2+i）=6-2i，则z是（　　）
A．2-2iB．$\sqrt{2}$-2iC．$\sqrt{3}$+iD．3+i
16．《莱因德纸草书》（Rhind Papyrus）是世界上最古老的数学著作之一，书中有这样一道题：把120个面包分成5份，使每份的面包数成等差数列，且较多的三份之和恰好是较少的两份之和的7倍，则最少的那份有（　　）个面包．
A．4B．3C．2D．1
17．在同一坐标系中，函数y=ax+b与y=logax的图象可以是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网