Question

函数f（x）=x³+bx²+cx+d，x∈（0，1）时取极大值，x∈（1，2）取极小值，则（b+

1

2

）²+（c-3）²的取值范围为

 

．

Answer 1

考点：利用导数研究函数的极值,简单线性规划的应用

专题：导数的综合应用,不等式的解法及应用

分析：据极大值点左边导数为正右边导数为负，极小值点左边导数为负右边导数为正得a，b的约束条件，据线性规划求出最值．

解答： 解：∵f（x）=x³+bx²+cx+d，
∴f′（x）=3x²+2bx+c，
∵函数f（x）在x∈（0，1）时取得极大值，当x∈（1，2）时取极小值，
∴f′（x）=3x²+2bx+c=0在（0，1）和（1，2）内各有一个根，
∴f′（0）＞0，f′（1）＜0，f′（2）＞0，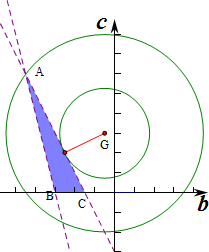
即

c＞0 3+2b+c＜0 12+4b+c＞0

，
作出不等式组对应的平面区域如图，
（b+

1

2

）²+（c-3）²的几何意义表示点G（-

1

2

，3）与可行域内的点连线的距离的平方，
点G（-

1

2

，3）到直线3+2b+c=0的距离为d=

|- 1 2 ×2+3+3|

22+1

=

5

5

=

5

，此时（b+

1

2

）²+（c-3）²最小为5，
由

12+4b+c=0 3+2b+c=0

，解得

b=- 9 2 c=6

，即A（-

9

2

，6），
此时AG的距离最大为AG=5，此时（b+

1

2

）²+（c-3）²最大为25，
∴（b+

1

2

）²+（c-3）²的取值范围是（5，25），
故答案为：（5，25）．

点评：本题主要考查利用导数研究函数极值的能力，根据函数导数的定义将条件转化为不等式组，利用线性规划的知识结合两点间的距离公式进行求解是解决本题的关键．综合性较强，有一定的难度．