题目内容
已知Sn为数列{an}的前n项和,Sn=nan-3n(n-1)(n∈N*),且a2=11.
(1)求a1的值;
(2)求数列{an}的前n项和Sn;
(3)设数列{bn}满足bn=
,求证:b1+b2+…+bn<
.
(1)求a1的值;
(2)求数列{an}的前n项和Sn;
(3)设数列{bn}满足bn=
|
| 2 |
| 3 |
| 3n+2 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知得S2=a1+a2=2a2-3×2(2-1),a2=11,由此能求出a1.
(2)当n≥2时,由an=Sn-Sn-1,得an=nan-3n(n-1)-(n-1)an-1-3(n-1)(n-2),从而得到数列{an}是首项a1=5,公差为6的等差数列,由此能求出数列{an}的前n项和Sn.
(3)由bn=
=
=
<
=
(
-
),由此能证明b1+b2+…+bn<
.
(2)当n≥2时,由an=Sn-Sn-1,得an=nan-3n(n-1)-(n-1)an-1-3(n-1)(n-2),从而得到数列{an}是首项a1=5,公差为6的等差数列,由此能求出数列{an}的前n项和Sn.
(3)由bn=
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
| 2 |
| 3 |
| 3n+2 |
| 3n-1 |
| 2 |
| 3 |
| 3n+2 |
解答:
解:(1)∵Sn=nan-3n(n-1)(n∈N*),且a2=11.
∴S2=a1+a2=2a2-3×2(2-1),
∵a2=11,解得a1=5.(2分)
(2)当n≥2时,由an=Sn-Sn-1,
得an=nan-3n(n-1)-(n-1)an-1-3(n-1)(n-2),(4分)
∴(n-1)an-(n-1)an-1=6(n-1),
∴an-an-1=6,n≥2,n∈N*,(6分)
∴数列{an}是首项a1=5,公差为6的等差数列,
∴an=a1+6(n-1)=6n-1,(7分)
∴Sn=
=3n2+2n.(8分)
(3)证明:∵bn=
=
=
<
(10分)
=
=
(
-
),(11分)
∴b1+b2+…+bn<
[(
-
)+(
-
)+…+(
-
)](13分)
=
(
-
)<
,
∴b1+b2+…+bn<
.(14分)
∴S2=a1+a2=2a2-3×2(2-1),
∵a2=11,解得a1=5.(2分)
(2)当n≥2时,由an=Sn-Sn-1,
得an=nan-3n(n-1)-(n-1)an-1-3(n-1)(n-2),(4分)
∴(n-1)an-(n-1)an-1=6(n-1),
∴an-an-1=6,n≥2,n∈N*,(6分)
∴数列{an}是首项a1=5,公差为6的等差数列,
∴an=a1+6(n-1)=6n-1,(7分)
∴Sn=
| n(a1+an) |
| 2 |
(3)证明:∵bn=
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
=
2(
| ||||||||
(
|
| 2 |
| 3 |
| 3n+2 |
| 3n-1 |
∴b1+b2+…+bn<
| 2 |
| 3 |
| 5 |
| 2 |
| 8 |
| 5 |
| 3n+2 |
| 3n-1 |
=
| 2 |
| 3 |
| 3n+2 |
| 2 |
| 2 |
| 3 |
| 3n+2 |
∴b1+b2+…+bn<
| 2 |
| 3 |
| 3n+2 |
点评:本题考查数列的首项的求法,考查数列的前n项和的求法,考查不等式的证明,是中档题,解题时要认真审题,注意等差数列的性质和放缩法的合理运用.

练习册系列答案
相关题目
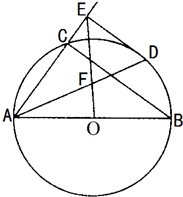 如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.
如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.