题目内容

一个等差数列的前20项的和为354，前20项中偶数项的和与奇数项的和之比为32：27，则该数列的公差d等于
 
．
考点：等差数列的性质
专题：等差数列与等比数列
分析：由题意，列出关于前20项中偶数项的和与奇数项的和的方程组，可解得它们的值，而S偶-S奇=10d，代入可解．
解答： 解：设首项为a1，公差为d，
则由题意可得
S奇+S偶=354
S奇
S偶
=
32
27
，
解得
S奇=192
S偶=162

又S偶-S奇=10d=30，
∴d=3．
故答案为：3．
点评：本题考查等差数列的性质和公差的定义，属基础题．
练习册系列答案
相关题目
已知等差数列{an}的公差和首项都不等于0，且a2、a4、a8成等比数列，则下列式子的值最小的是（　　）
A、
a2
a1
B、
a3
a2
C、
a4
a3
D、
a5
a4
已知F（x）=f（x）-g（x），其中f（x）=2loga（4-x）（a＞0且a≠1），并且当且仅当点P（x0，y0）在f（x）的图象上时，点Q（-
1
5
x0，
1
2
y0）在y=g（x）的图象上．
（1）求y=g（x）的解析式；
（2）解关于x的不等式F（x）≥0．
已知椭圆的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），过椭圆右焦点且与x轴垂直的直线与椭圆交于P、Q两点，x轴一点M（
a2
c
，0），若△PQM为正三角形，则椭圆的离心率等于
 
．
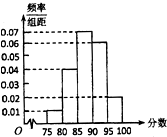某次有1000人参加数学摸底考试，其成绩的频率分布直方图如题（16）图所示，规定85分及以上为优秀．
（1）下表是这次考试成绩的频数分布表，求正整数a，b的值；
区间[75，80）[80，85）[85，90）[90，95）[95，100]
人数50a350300b
（2）某文科班数学老师抽取10名同学的数学成绩对该科进行抽样分析，得到第i个同学每天花在数学上的学习时间xi（单位：小时）与数学考试成绩yi（单位：百分）的数据资料，算得
10
i=1
xi=15，
10
i=1
yi=10，
10
i=1
xiyi=16，
10
i=1
x_2 =25，求数学考试成绩y对每天花在数学上的学习时间x的线性回归方程
y
=bx+a；
附：线性回归方程y=bx+a中，b=
n
i=1
xiyi-n
.
x
.
y
n
i=1
x
2
i
-n\mathopxlimits-2
，a=
.
y
-b
.
x
．
已知变量x，y满足
x≥2
x+y-4≤0
x-y-1≤0
，则
y
x
的最大值是
 
．
设函数f（x）=
x2+x，x＜0
-x2，x≥0
，若f（f（a））≤2，则实数a的取值范围是
 
．
已知
a
，
b
，
c
为非0向量，则“
a
b
=
a
c
”是“
b
=
c
”的充要条件是否为真命题，为什么？
一个三棱锥的三视图如图，则其体积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网