题目内容
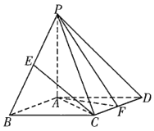
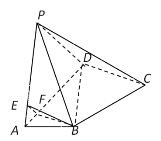
【题目】如图,在四棱锥![]() ABCD中,
ABCD中,![]() 和
和![]() 都是等边三角形,平面PAD
都是等边三角形,平面PAD![]() 平面ABCD,且
平面ABCD,且![]() ,
,![]() .
.
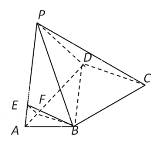
(1)求证:CD![]() PA;
PA;
(2)E,F分别是棱PA,AD上的点,当平面BEF//平面PCD时,求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由已知即可证得:![]() ,且
,且![]() ,再利用
,再利用![]() 是等边三角形即可证得:
是等边三角形即可证得:![]() ,再利用面面垂直的性质即可证得:
,再利用面面垂直的性质即可证得:![]() 平面
平面![]() ,问题得证.
,问题得证.
(2)利用平面BEF//平面PCD可得:BF//CD,结合![]() 可得
可得![]() ,即可求得:DF=
,即可求得:DF=![]() ,从而求得
,从而求得![]() ,利用(1)可得四棱锥
,利用(1)可得四棱锥![]() 的高
的高![]() ,再利用锥体体积公式计算即可.
,再利用锥体体积公式计算即可.
证明:(1)因为![]() 是等边三角形,所以
是等边三角形,所以![]()
又![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,且
,且![]() .
.
又![]() 是等边三角形,所以
是等边三角形,所以![]() ,
,
所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
所以CD![]() PA.
PA.
(2)因为平面BEF//平面PCD,
所以BF//CD,EF//PD,又![]()
所以![]() .
.
又在直角三角形ABD中,DF=![]() ,
,
所以![]() .
.
所以![]() .
.
由(1)知![]() 平面
平面![]() ,故四棱锥
,故四棱锥![]() 的体积
的体积![]() .
.

练习册系列答案
相关题目